题目内容
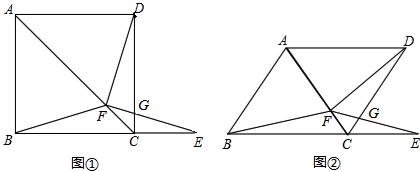
12. 如图已知,OM平分∠AOB,点D,C分别在OM,OA上,∠COD=∠CDO,求证:CD∥OB.
如图已知,OM平分∠AOB,点D,C分别在OM,OA上,∠COD=∠CDO,求证:CD∥OB.
分析 欲证明CD∥OB,只需推知∠CDO=∠BOD即可.
解答  证明:如图,∵OM平分∠AOB,
证明:如图,∵OM平分∠AOB,
∴∠AOM=∠BOM,即∠COD=∠BOD.
又∵∠COD=∠CDO,
∴∠CDO=∠BOD,
∴CD∥OB.
点评 本题考查了平行线的判定.定理1:同位角相等,两直线平行.
定理2:内错角相等,两直线平行.
定理3:同旁内角互补,两直线平行.
定理4:两条直线都和第三条直线平行,那么这两条直线平行.
定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.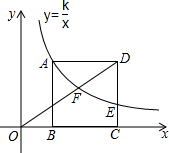 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )| A. | ($\frac{2\sqrt{3}}{3},\sqrt{3}$) | B. | ($\sqrt{3},\frac{2\sqrt{3}}{3}$) | C. | ($\frac{\sqrt{3}}{3},2\sqrt{3}$) | D. | (2$\sqrt{3},\frac{\sqrt{3}}{3}$) |
3.矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AC=6,则△ABO的周长为( )
| A. | 18 | B. | 15 | C. | 12 | D. | 9 |
7.已知不等式2x+a<3x的解为x>1,则a的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
1.下列汽车标志中,可以看作中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,a∥b,∠2=100°,则∠1的度数为80°.
如图,a∥b,∠2=100°,则∠1的度数为80°.