题目内容
设a、b、c为△ABC的三边,且满足a>b>c,2b=a+c,a2+b2+c2=84,求正整数b的值.
考点:三角形边角关系
专题:
分析:根据2b=a+c,a2+b2+c2=84可以得到2b=a+c,2ac=4b2-a2-c2,根据均值不等式即可得到b2≤28,从而求得b的可能取值,然后进行排除即可.
解答:解:∵4b2=a2+2ac+c2,b2=84-a2-c2,
∴2b=a+c,2ac=4b2-a2-c2.
∵a>0,c>0,由均值不等式,a2+c2≥2ac,即a2+c2≥4b2-a2-c2,
∴a2+c2≥2b2.
∵a2+b2+c2=84,
∴84≥2b2+b2=3b2,
解得:b2≤28,
又∵b是正整数,
∴b的可能取值是5,4,3,2,1.
若b=3,则c<3,a<b+c<6.
则a2+b2+c2<54<84,
∴b>3,即b可能取值是4或5.
若b=4,则a+c=2b=8,a2+16+c2=84,
联立上边的两式得:c=10>b.
∴b≠4.
∴b=5.
∴2b=a+c,2ac=4b2-a2-c2.
∵a>0,c>0,由均值不等式,a2+c2≥2ac,即a2+c2≥4b2-a2-c2,
∴a2+c2≥2b2.
∵a2+b2+c2=84,
∴84≥2b2+b2=3b2,
解得:b2≤28,
又∵b是正整数,
∴b的可能取值是5,4,3,2,1.
若b=3,则c<3,a<b+c<6.
则a2+b2+c2<54<84,
∴b>3,即b可能取值是4或5.
若b=4,则a+c=2b=8,a2+16+c2=84,
联立上边的两式得:c=10>b.
∴b≠4.
∴b=5.
点评:本题考查了三角形的三边关系以及均值不等式,正确求得b的可能取值是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
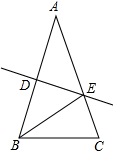 已知如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于点D、E.
已知如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于点D、E. 如图,从一个大正方形中裁去面积为15cm2和24cm2的两个小正方形,求留下部分(即阴影部分)的面积.
如图,从一个大正方形中裁去面积为15cm2和24cm2的两个小正方形,求留下部分(即阴影部分)的面积.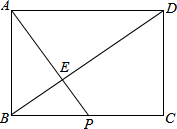 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=