Question

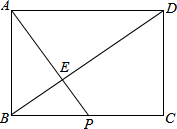如图，在矩形ABCD中，AB=

3

，AD=

6

，P是BC的中点，AP和BD相交于点E，
（1）求证：AP⊥BD；
（2）求四边形PCDE的面积．

Answer 1

考点：矩形的性质,勾股定理,相似三角形的判定与性质

专题：

分析：（1）根据“平行线法”证得△ADE∽△PBE，由该相似三角形的对应边成比例和勾股定理的逆定理证得结论；
（2）利用“S_{四边形PCDE}=S_△BCD-S_△BPE”进行解答．

解答：（1）证明：如图，连接PD．
∵四边形ABCD是矩形，
∴AD∥BC，AD=BC=

6

，∠BAD=90°，
∴由勾股定理得到：BD=

AB2+AD2

=3，且△ADE∽△PBE．
∵点P是BC的中点，
∴BP=

1

2

AB=

6

2

，
∴在直角△ABP中，由勾股定理得到：AP=

AB2+BP2

=

3+ 3 2

=

3 2

2

．
∵△ADE∽△PBE，
∴

AD

BP

=

AE

PE

=

DE

BE

=

2

1

=2，
∴AE=2PE=

2

3

AP=

2

，PE=

2

2

，DE=2BE=

2

3

BD=2，故BE=1．
∴AE²+BE²=AB²=6，
∴AP⊥BD；

（2）解：S_{四边形PCDE}=S_△BCD-S_△BPE
=

1

2

DC•BC-

1

2

BE•PE
=

1

2

×

3

×

6

-

1

2

×1×

2

2

=

5 2

4

．

点评：本题考查了矩形的性质，相似三角形的判定与性质，勾股定理．解答（2）题时，利用了分割法．