题目内容
11. 如图,要在河边修建一个水泵站,分别向A村、B村送水,已知:A、B到直线l的距离分别是1km和3km,两点的水平距离为3km,要在直线l上找到一个点P,使PA+PB得和最小,请在图中找出点P的位置,并计算PA+PB的最小值.
如图,要在河边修建一个水泵站,分别向A村、B村送水,已知:A、B到直线l的距离分别是1km和3km,两点的水平距离为3km,要在直线l上找到一个点P,使PA+PB得和最小,请在图中找出点P的位置,并计算PA+PB的最小值.
分析 作点A关于直线l的对称点A′,连接BA′与直线l交于点P,此时PA+PB最小,在RT△A′BN中利用勾股定理求出线段A′B即可.
解答 解:如图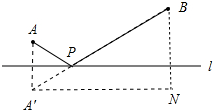 作点A关于直线l的对称点A′,连接BA′与直线l交于点P,此时PA+PB最小.
作点A关于直线l的对称点A′,连接BA′与直线l交于点P,此时PA+PB最小.
作A′N∥l,BN⊥l两条线交于点N,
在RT△A′BN中,∵A′N=3,BN=1+3=4,
∴A′B=$\sqrt{A′{N}^{2}+B{N}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵PA=PB=PA′+PB=A′B=5,
∴PA+PB的最小值为5.
点评 本题考查轴对称-最短问题、勾股定理等知识,利用对称找到点P的位置是解题的关键,属于中考常考题型.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
16.已知⊙O外一点A到圆的最大距离为18cm,到圆的最小距离为8cm,则这个圆的半径为( )
| A. | 4cm | B. | 5cm | C. | 8cm | D. | 9cm |

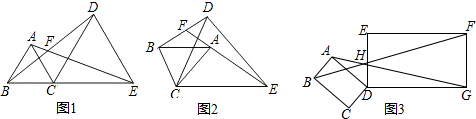
 如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$.
如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$.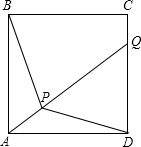 如图,点P是正方形ABCD内一点,并延长AP与DC相交于点Q.
如图,点P是正方形ABCD内一点,并延长AP与DC相交于点Q.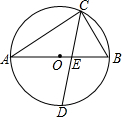 如图,AB为⊙O的直径,弦CD平分圆周角∠ACB,交AB于E,若AC=2BC,求$\frac{CE}{DE}$的值.
如图,AB为⊙O的直径,弦CD平分圆周角∠ACB,交AB于E,若AC=2BC,求$\frac{CE}{DE}$的值.