题目内容
12. 如图,将Rt△ABC绕直角顶点A顺时针旋转90°,得到△AB′C′,连结BB′,若∠1=25°,则∠C的度数是70°.
如图,将Rt△ABC绕直角顶点A顺时针旋转90°,得到△AB′C′,连结BB′,若∠1=25°,则∠C的度数是70°.
分析 根据旋转的性质可得AB=AB′,然后判断出△ABB′是等腰直角三角形,根据等腰直角三角形的性质可得∠ABB′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠B′C′A,然后根据旋转的性质可得∠C=∠B′C′A.
解答 解:∵Rt△ABC绕直角顶点A顺时针旋转90°得到△AB′C′,
∴AB=AB′,
∴△ABB′是等腰直角三角形,
∴∠ABB′=45°,
∴∠AC′B′=∠1+∠ABB′=25°+45°=70°,
由旋转的性质得∠C=∠AC′B′=70°.
故答案为:70°.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
1.已知关于x的不等式组$\left\{\begin{array}{l}{2x+m>0}\\{x-1<6}\end{array}\right.$有五个整数解,m的取值范围是( )
| A. | -4≤m<-2 | B. | -4<m<-2 | C. | -4<m≤-2 | D. | -4≤m≤-2 |
2.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2015=( )
| A. | (31,50) | B. | (32,47) | C. | (33,46) | D. | (34,42) |
 如图,在矩形ABCD的对角线AC上取两点E和F,且AE=CF,求证:DF=BE.
如图,在矩形ABCD的对角线AC上取两点E和F,且AE=CF,求证:DF=BE.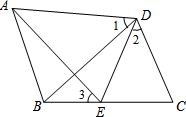 已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由.
已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由. “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.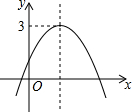 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论: