题目内容
7.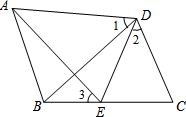 已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由.
已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由.解:因为∠1=∠2(已知),
所以∠1+∠BDE=∠2+∠BDE(等式性质),
即∠ADE=∠BDC.
在△ADE和△BDC中,
$\left\{\begin{array}{l}{AD=BD(已知)}\\{∠()=∠()}\\{ED=CD(已知)}\end{array}\right.$所以△ADE≌△BDC(SAS).
所以∠AED=∠C(全等三角形对应角相等).
又因为∠BED=∠2+∠C(三角形的一个外角等于与它不相邻的两个内角的和),
即∠3+∠AED=∠2+∠C,
所以∠3=∠2(等式的性质).
因为∠1=∠2(已知),
所以∠3=∠1(等量代换).
分析 如图,首先运用等式的基本性质证明∠ADE=∠BDC;运用SAS公理证明△ADE≌△BDC,借助全等三角形的性质证明∠AED=∠C;借助三角形外角的性质及等式的基本性质,即可证明∠3=∠1.
解答  解:因为∠1=∠2(已知),
解:因为∠1=∠2(已知),
所以∠1+∠BDE=∠2+∠BDE(等式性质),
即∠ADE=∠BDC.
在△ADE和△BDC中,
$\left\{\begin{array}{l}{AD=BD}\\{∠ADE=∠BDC}\\{ED=CD}\end{array}\right.$,
所以△ADE≌△BDC(SAS).
所以∠AED=∠C ( 全等三角形对应角相等 ).
又因为∠BED=∠2+∠C( 三角形的一个外角等于与它不相邻的两个内角的和 ),
即∠3+∠AED=∠2+∠C,
所以∠3=∠2( 等式的性质 ).
因为∠1=∠2(已知),
所以∠3=∠1( 等量代换 ).
点评 该题主要考查了等式的性质、三角形外角的性质、全等三角形的判定等几何知识点及其应用问题;应牢固掌握三角形外角的性质、全等三角形的判定等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
17.某班九名同学在篮球场进行定点投篮测试,每人投篮五次,投中的次数统计如下:6,3,2,6,6,1,5,0,3,则这组数据的中位数、众数分别为( )
| A. | 3.6 | B. | 4.3 | C. | 3.3 | D. | 4.4 |
18.下列几何体中,俯视图为矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.若kb>0,且不等式kx+b>0的解集是x<-$\frac{b}{k}$,则下列判断正确的是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
 如图,将Rt△ABC绕直角顶点A顺时针旋转90°,得到△AB′C′,连结BB′,若∠1=25°,则∠C的度数是70°.
如图,将Rt△ABC绕直角顶点A顺时针旋转90°,得到△AB′C′,连结BB′,若∠1=25°,则∠C的度数是70°.
 如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.