题目内容
10. 如图,已知AD为△ABC的角平分线,AD的垂直平分线交BC延长线于点F,交AB于点E.求证:
如图,已知AD为△ABC的角平分线,AD的垂直平分线交BC延长线于点F,交AB于点E.求证:(1)△BAF∽△ACF;
(2)AB2:AC2=BF:CF.
分析 (1)利用垂直平分线的性质得出AF=DF,进而利用外角的性质得出∠B=∠1,即可得出△ACF∽△BAF,即可得出答案;
(2)利用(1)中所求由相似三角形的性质得出即可.
解答 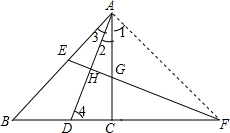 证明:(1)连接AF,
证明:(1)连接AF,
∵AD的垂直平分线交BC的延长线于F,
∴AF=DF,
∴∠1+∠2=∠4,
∵∠B+∠3=∠4,
∠2=∠3,
∴∠B=∠1,
∵∠AFB=∠CFA,
∴△ACF∽△BAF;
(2)∵△ACF∽△BAF,
∴$\frac{AB}{AC}$=$\frac{AF}{CF}$=$\frac{BF}{AF}$,
∴AF2=FB•FC,
∴$\frac{A{B}^{2}}{A{C}^{2}}$=$\frac{A{F}^{2}}{C{F}^{2}}$=$\frac{FB}{CF}$.
点评 此题主要考查了相似三角形的判定与性质,根据已知得出∠B=∠1是解题关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
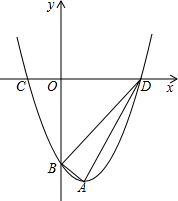 如图,抛物线y=x2-2x-3的顶点为A,与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状.
如图,抛物线y=x2-2x-3的顶点为A,与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状.
 如图是一个抛物线形拱桥,量得两个数据,则会以抛物线顶点为原点建立直角坐标系,并求得其解析式为y=-0.03x2.
如图是一个抛物线形拱桥,量得两个数据,则会以抛物线顶点为原点建立直角坐标系,并求得其解析式为y=-0.03x2.