Question

18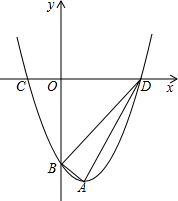．如图，抛物线y=x²-2x-3的顶点为A，与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状．

Answer 1

分析 根据抛物线解析式求得点A、B、D的坐标．则AB、AD、BD三边的长可得，然后根据边长确定三角形的形状．

解答 解：△ABD是直角三角形，理由如下：
∵y=x²-2x-3=（x-1）²-4，
∴A（1，-4）．
∵y=x²-2x-3=（x-3）（x+1），
∴D（3，0）．
令x=0，则y=-3，
∴B（0，-3），
∴BD²=OB²+OD²=18，AB²=（4-3）²+1²=2，AD²=（3-1）²+4²=20，
BD²+AB²=AD²，
∴∠ABD=90°，即△ABD是直角三角形．

点评 本题考查了抛物线与x轴的交点坐标．解题时，需要熟悉抛物线与坐标轴交点的求法、勾股定理的逆定理等知识点．