题目内容
5．
红丝带是关注艾滋病防止问题的国际性标志，人们将等宽红丝带剪成小段，并用别针将折叠好的红丝带别在胸前，图中红丝带重叠部分形成的图形一定是菱形．
分析 首先可判断重叠部分为平行四边形，且两条彩带宽度相同；再由平行四边形的面积可得邻边相等，则重叠部分为菱形．
解答 解：如图所示：过点A作AE⊥BC于E，AF⊥CD于F，
因为两条彩带宽度相同，
所以AB∥CD，AD∥BC，AE=AF．
∴四边形ABCD是平行四边形．
∵S?ABCD=BC•AE=CD•AF．又AE=AF．
∴BC=CD，
∴四边形ABCD是菱形．
故答案为：菱形．
点评 本题利用了平行四边形的判定和平行四边形的面积公式、一组邻边相等的平行四边形是菱形．
练习册系列答案
阅读快车系列答案
相关题目
20．如图图案不是轴对称图形的有（ ）个． 
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
14．
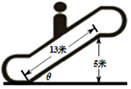如下图，某超市的自动扶梯长度为13米，该自动扶梯到达的最大高度是5米，设自动扶梯与地面所成的角为θ，则tanθ=（ ）
如下图，某超市的自动扶梯长度为13米，该自动扶梯到达的最大高度是5米，设自动扶梯与地面所成的角为θ，则tanθ=（ ）| A． | $\frac{5}{13}$ | B． | $\frac{13}{12}$ | C． | $\frac{5}{12}$ | D． | $\frac{12}{5}$ |
15．
如图，∠BAC=90°，AD⊥BC，则图中互余的角有（ ）
如图，∠BAC=90°，AD⊥BC，则图中互余的角有（ ）| A． | 2对 | B． | 3对 | C． | 4对 | D． | 5对 |