题目内容
14.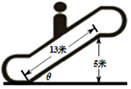 如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )
如下图,某超市的自动扶梯长度为13米,该自动扶梯到达的最大高度是5米,设自动扶梯与地面所成的角为θ,则tanθ=( )| A. | $\frac{5}{13}$ | B. | $\frac{13}{12}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
分析 在Rt△ABC中利用勾股定理求得BC的长,然后根据正切函数的定义求解.
解答  解:在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
解:在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
则tanθ=$\frac{BC}{AC}$=$\frac{5}{12}$.
故选C.
点评 本题考查了勾股定理和三角函数的定义,正确记忆正切函数的定义是关键.

练习册系列答案
相关题目
4.若$\sqrt{(3-b)^{2}}$=3-b,则b满足的条件是( )
| A. | b>3 | B. | b<3 | C. | b≥3 | D. | b≤3 |
2.在图中,互相全等的平行四边形按一定的规律排列.其中,第①个图形中有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,…,则第⑥个图形中平行四边形的个数为( )个.


| A. | 41 | B. | 110 | C. | 19 | D. | 109 |
19.平面直角坐标系中,△ABC关于y轴的对称图形是△A'B'C',若BC边上有点P(a,b),则它的对应点P'的坐标为( )
| A. | (a,b) | B. | (a,-b) | C. | (-a,b) | D. | (-a,-b) |
3.已知A、B两地实际距离是250米,图上距离是5厘米,则这幅地图的比例尺为( )
| A. | 1:50 | B. | 1:5000 | C. | 1:500 | D. | 1:50000 |
4.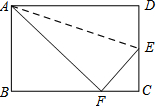 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )
 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC的长( )| A. | 3 cm | B. | 4 cm | C. | 5 cm | D. | 6 cm |
 红丝带是关注艾滋病防止问题的国际性标志,人们将等宽红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,图中红丝带重叠部分形成的图形一定是菱形.
红丝带是关注艾滋病防止问题的国际性标志,人们将等宽红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,图中红丝带重叠部分形成的图形一定是菱形.