题目内容
多项式-2x2y3z+xy2-5是______次_______ 项式。
 六 三
【解析】∵-2x2y3z的次数是6,xy2的次数是3,-5的次数是0,
∴多项式-2x2y3z+xy2-5是六次三项式。
六 三
【解析】∵-2x2y3z的次数是6,xy2的次数是3,-5的次数是0,
∴多项式-2x2y3z+xy2-5是六次三项式。
练习册系列答案
相关题目
小胡将一枚质地均匀的硬币抛掷了10次,正面朝上的情况出现了6次,若用A表示正面朝上这一事件,则事件A发生的( )
A. 频率是0.4 B. 频率是0.6
C. 频率是6 D. 频率接近0.6
 B
【解析】总共抛10次硬币,正面朝上的次数为6次,那么正面朝上的概率是,即0.6,而频率则无法估算.
故答案为:B.
B
【解析】总共抛10次硬币,正面朝上的次数为6次,那么正面朝上的概率是,即0.6,而频率则无法估算.
故答案为:B. 当x=2时,代数式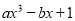 的值等于-9,那么当x=-1时,代数式 16ax-4bx3-2的值等于______.
的值等于-9,那么当x=-1时,代数式 16ax-4bx3-2的值等于______.
 18
【解析】把x=2代入=-9中,
得:8a-2b+1=-9
整理,得:4a-b=-5.
把x=-1代入16ax-4bx3-2中,
得:-16a+4b-2=-4(a-b)-2=-4×(-5)-2=18.
18
【解析】把x=2代入=-9中,
得:8a-2b+1=-9
整理,得:4a-b=-5.
把x=-1代入16ax-4bx3-2中,
得:-16a+4b-2=-4(a-b)-2=-4×(-5)-2=18. 化简或求值:(①小题4分,②小题6分,共10分)
(1)化简: 7 mn-6m-2n-(4mn+3m-2n)
(2)先化简,再求值。求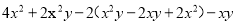 的值.
的值.
已知: 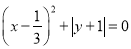
 (1)3mn-9m ;(2)3xy=-1
【解析】试题分析:(1)先去括号,然后合并同类项;(2)先根据绝对值和偶次方的非负性求出x和y的值,再把所给代数式去括号合并同类项化简,然后代入求值.
【解析】
(1)7mn-6m-2n-(4mn+3m-2n)
=7mn-6m-2n-4mn-3m+2 n
=3mn-9 m;
(2)∵,
∴=0, =0,
∴, ,...
(1)3mn-9m ;(2)3xy=-1
【解析】试题分析:(1)先去括号,然后合并同类项;(2)先根据绝对值和偶次方的非负性求出x和y的值,再把所给代数式去括号合并同类项化简,然后代入求值.
【解析】
(1)7mn-6m-2n-(4mn+3m-2n)
=7mn-6m-2n-4mn-3m+2 n
=3mn-9 m;
(2)∵,
∴=0, =0,
∴, ,... 下面的计算正确的是( )
A. 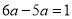 B.
B. 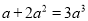 C.
C. 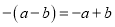 D.
D. 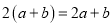
 C
【解析】A. ∵,故不正确;
B. ∵a与不是同类项,不能合并 ,故不正确;
C. ∵,故正确;
D. ∵,故不正确;
故选C.
C
【解析】A. ∵,故不正确;
B. ∵a与不是同类项,不能合并 ,故不正确;
C. ∵,故正确;
D. ∵,故不正确;
故选C. 如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
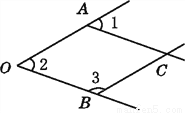
 证明见解析.
【解析】试题分析:根据已知可得∠1=∠2,∠2+∠3=180°,由同位角相等,两直线平行即可得OB∥AC,由同旁内角互补,两直线平行可得OA∥BC.
试题解析:
OA∥BC,OB∥AC,理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2,
∴OB∥AC,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥B...
证明见解析.
【解析】试题分析:根据已知可得∠1=∠2,∠2+∠3=180°,由同位角相等,两直线平行即可得OB∥AC,由同旁内角互补,两直线平行可得OA∥BC.
试题解析:
OA∥BC,OB∥AC,理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2,
∴OB∥AC,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥B... 如图,∠B=∠C,B、A、D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线.
求证:AE∥BC.
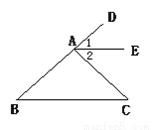
 见解析.
【解析】试题分析:先根据∠B=∠C,∠DAC=∠B+∠C得出∠DAC=2∠B,再由AE是∠DAC的平分线可知∠1=∠2,∠DAC=2∠1,故∠1=∠B,由此可得出结论.
试题解析:∵AE是∠DAC的平分线
∴∠DAC=2∠1
∵∠DAC=∠B+∠C,∠B=∠C
∴∠DAC=2∠B
∴∠1=∠B
∴AE∥BC
见解析.
【解析】试题分析:先根据∠B=∠C,∠DAC=∠B+∠C得出∠DAC=2∠B,再由AE是∠DAC的平分线可知∠1=∠2,∠DAC=2∠1,故∠1=∠B,由此可得出结论.
试题解析:∵AE是∠DAC的平分线
∴∠DAC=2∠1
∵∠DAC=∠B+∠C,∠B=∠C
∴∠DAC=2∠B
∴∠1=∠B
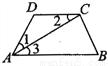
∴AE∥BC 如图,已知AB=CD,AC=BD,说明AD∥BC。
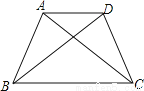
 证明见解析
【解析】试题分析:由SSS证明△ABC≌△DCB,得出对应角相等∠ACB=∠DBC,同理:∠ADB=∠DAC,由三角形外角关系证出∠DAC=∠ACB,即可得出AD∥BC.
试题解析:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,
同理:∠ADB=∠DAC,
∵∠ACB+∠DBC=∠ADB+∠DAC,
...
证明见解析
【解析】试题分析:由SSS证明△ABC≌△DCB,得出对应角相等∠ACB=∠DBC,同理:∠ADB=∠DAC,由三角形外角关系证出∠DAC=∠ACB,即可得出AD∥BC.
试题解析:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,
同理:∠ADB=∠DAC,
∵∠ACB+∠DBC=∠ADB+∠DAC,
...