题目内容
当x=2时,代数式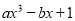 的值等于-9,那么当x=-1时,代数式 16ax-4bx3-2的值等于______.
的值等于-9,那么当x=-1时,代数式 16ax-4bx3-2的值等于______.
 18
【解析】把x=2代入=-9中,
得:8a-2b+1=-9
整理,得:4a-b=-5.
把x=-1代入16ax-4bx3-2中,
得:-16a+4b-2=-4(a-b)-2=-4×(-5)-2=18.
18
【解析】把x=2代入=-9中,
得:8a-2b+1=-9
整理,得:4a-b=-5.
把x=-1代入16ax-4bx3-2中,
得:-16a+4b-2=-4(a-b)-2=-4×(-5)-2=18.
练习册系列答案
相关题目
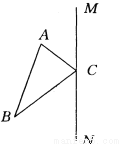
如图所示,已知△ABC和直线MN.求作:△A′B′C,使△A′B′C和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
 作图见解析.
【解析】
试题分析:要作出一个三角形关于直线对称,只需要作出三个顶点关于这条直线的对称点,然后连接这三个对称点即可,如图,过点A作MN的垂线交MN与点K,延长AK至点A′,使得AK= A′K, 点A′是点A关于MN的对称点, 过点B作MN的垂线交MN与点L,延长BL至点B′,使得BL= B′L, 点B′是点B关于MN的对称点, 点C关于MN的对称点就是点C,连接A′B′C...
作图见解析.
【解析】
试题分析:要作出一个三角形关于直线对称,只需要作出三个顶点关于这条直线的对称点,然后连接这三个对称点即可,如图,过点A作MN的垂线交MN与点K,延长AK至点A′,使得AK= A′K, 点A′是点A关于MN的对称点, 过点B作MN的垂线交MN与点L,延长BL至点B′,使得BL= B′L, 点B′是点B关于MN的对称点, 点C关于MN的对称点就是点C,连接A′B′C... (12分)若a、b互为相反数,b、c互为负倒数,并且m的立方等于它本身.
(1)试求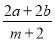 ﹣ac值;
﹣ac值;
(2)若a>1,且m=﹣1,S=|2a﹣3b|﹣2|b﹣m|﹣|b+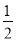 |,试求4(2a﹣S)+2(2a﹣S)﹣(2a﹣S)的值.
|,试求4(2a﹣S)+2(2a﹣S)﹣(2a﹣S)的值.
(3)若m>0,且x为有理数时,|x+m|﹣|x﹣m|+1是否存在最大值,若存在,求出这个最大值,并求出x的取值范围;若不存在,请说明理由.
 (1)-1;(2);(3)当x时,取最大值为3
【解析】试题分析:(1)先根据a、b互为相反数,b、c互为倒数,得出a+b=0,bc=1,再代入所求代数式进行计算;
(2)根据a>1及m的立方等于它本身把S进行化简,再代入所求代数式进行计算;
(3)根据若m>0,可知m=1,当m=1时,代入|x+m|-|x-m|+1,再根据绝对值的性质去掉绝对值符号,求出代数式的值;
【解...
(1)-1;(2);(3)当x时,取最大值为3
【解析】试题分析:(1)先根据a、b互为相反数,b、c互为倒数,得出a+b=0,bc=1,再代入所求代数式进行计算;
(2)根据a>1及m的立方等于它本身把S进行化简,再代入所求代数式进行计算;
(3)根据若m>0,可知m=1,当m=1时,代入|x+m|-|x-m|+1,再根据绝对值的性质去掉绝对值符号,求出代数式的值;
【解... (8分)如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数.
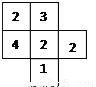
(1)请画出这个几何体的主视图、左视图。
(2)若小立方体的棱长为2cm,求该几何体的表面积。
 (1)见解析;(2)184
【解析】试题分析:(1)从正面看有三列,左侧有4行,中间有3行,右侧有2行;从左面看有三列,左侧有3行,中间有4行,右侧有1行;(2)用一个正方形的面积4乘以漏出的小正方形面的个数46即可.
【解析】
(1)如图,
(2)4×(9×2+8×2×+6×2)=184cm2.
(1)见解析;(2)184
【解析】试题分析:(1)从正面看有三列,左侧有4行,中间有3行,右侧有2行;从左面看有三列,左侧有3行,中间有4行,右侧有1行;(2)用一个正方形的面积4乘以漏出的小正方形面的个数46即可.
【解析】
(1)如图,
(2)4×(9×2+8×2×+6×2)=184cm2. 多项式-2x2y3z+xy2-5是______次_______ 项式。
 六 三
【解析】∵-2x2y3z的次数是6,xy2的次数是3,-5的次数是0,
∴多项式-2x2y3z+xy2-5是六次三项式。
六 三
【解析】∵-2x2y3z的次数是6,xy2的次数是3,-5的次数是0,
∴多项式-2x2y3z+xy2-5是六次三项式。 如图,点E在BC的延长线上,下列条件中能判定BC//AD的是 ( )
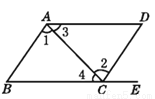
A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE
 C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C.
C
【解析】A. ∵∠1=∠2 ,∴AB∥CD, 故不正确;
B. ∵ ∠DAB+∠D=180° ,∴AB∥CD, 故不正确;
C. ∵∠3=∠4 ,∴ BC∥AD, 故正确;
D. ∵∠B=∠DCE,∴AB∥CD, 故不正确;
故选C. 如图,为了测量出池塘两端A,B之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度就得到了A,B两点之间的距离.你能说明其中的道理吗?
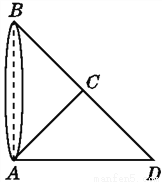
 证明见解析.
【解析】试题分析:根据SAS即可证明△ACB≌△ACD,由此即可解决问题.
试题解析:因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD.
证明见解析.
【解析】试题分析:根据SAS即可证明△ACB≌△ACD,由此即可解决问题.
试题解析:因为∠ACB=90°,所以∠ACD=180°-∠ACB=90°.
在△ABC和△ADC中,
所以△ABC≌△ADC(SAS).
所以AB=AD. 

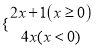 当x=2时,函数值y为()
当x=2时,函数值y为()