题目内容
小胡将一枚质地均匀的硬币抛掷了10次,正面朝上的情况出现了6次,若用A表示正面朝上这一事件,则事件A发生的( )
A. 频率是0.4 B. 频率是0.6
C. 频率是6 D. 频率接近0.6
B
【解析】总共抛10次硬币，正面朝上的次数为6次，那么正面朝上的概率是，即0.6，而频率则无法估算.
故答案为：B.
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
某人在做掷硬币试验时,投掷m次,正面朝上有n次
,则下列说法中正确的是( )
A. P一定等于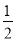
B. P一定不等于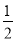
C. 多投一次,P更接近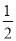
D. 随投掷次数逐渐增加,P在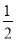
附近摆动
D
【解析】利用频率估计概率时，只有大量试验，才能用频率估计概率。因为硬币只有正反两面，所以投掷时正面朝上的概率为。因此随着投掷次数逐渐增加，稳定在附近.
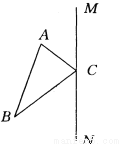
故选D. 如图所示，已知△ABC和直线MN．求作：△A′B′C，使△A′B′C和△ABC关于直线MN对称．（不要求写作法，只保留作图痕迹）
作图见解析.
【解析】
试题分析：要作出一个三角形关于直线对称,只需要作出三个顶点关于这条直线的对称点,然后连接这三个对称点即可,如图,过点A作MN的垂线交MN与点K,延长AK至点A′,使得AK= A′K, 点A′是点A关于MN的对称点, 过点B作MN的垂线交MN与点L,延长BL至点B′,使得BL= B′L, 点B′是点B关于MN的对称点, 点C关于MN的对称点就是点C,连接A′B′C... （12分）若a、b互为相反数，b、c互为负倒数，并且m的立方等于它本身．
（1）试求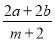
﹣ac值；
（2）若a＞1，且m=﹣1，S=|2a﹣3b|﹣2|b﹣m|﹣|b+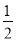
|，试求4（2a﹣S）+2（2a﹣S）﹣（2a﹣S）的值．
（3）若m＞0，且x为有理数时，|x+m|﹣|x﹣m|+1是否存在最大值，若存在，求出这个最大值，并求出x的取值范围；若不存在，请说明理由．
（1）-1；（2）；（3）当x时,取最大值为3
【解析】试题分析：（1）先根据a、b互为相反数，b、c互为倒数，得出a+b=0，bc=1，再代入所求代数式进行计算；
（2）根据a＞1及m的立方等于它本身把S进行化简，再代入所求代数式进行计算；
（3）根据若m>0，可知m=1，当m=1时，代入|x+m|-|x-m|+1，再根据绝对值的性质去掉绝对值符号，求出代数式的值；
【解... 多项式－2x2y3z+xy2-5是______次_______ 项式。
六 三
【解析】∵－2x2y3z的次数是6，xy2的次数是3，-5的次数是0，
∴多项式－2x2y3z+xy2-5是六次三项式。 如图,与∠B是同旁内角的角有( )
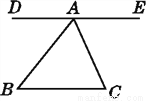
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】与∠B是同旁内角的角有∠C, ∠BAC, ∠BAE共3个.
故选C.