题目内容
18.已知,某等腰三角形的周长为12cm,设其底边长为ycm,腰长为xcm.(1)写出y与x的函数关系式,并指出自变量x的取值范围;
(2)画出这个函数的图象.
分析 (1)根据等腰三角形周长公式可求出底边长与腰的函数关系式,由三角形两边之和大于第三边的关系可知x的取值范围;
(2)根据函数关系式及自变量取值范围可画出函数图象.
解答  解:(1)因为等腰三角形周长为12,根据等腰三角形周长公式可求出底边长y与腰x的函数关系式为:
解:(1)因为等腰三角形周长为12,根据等腰三角形周长公式可求出底边长y与腰x的函数关系式为:
y=12-2x,
由三角形两边之和大于第三边的关系可知:y<2x,2x<12,
即得12-2x<2x,x<6.
故3<x<6;
(2)函数y=12-2x,3<x<6的图象为:
点评 此题主要考查了一次函数的应用以及等腰三角形的周长及三边的关系,得出y与x的函数关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.列方程解应用题:为了保护环境,节约用水,深圳按照《关于调整市水务(集团)有限公司自来水价格的通知》(深发改{2011}459 号)规定对供水范围内的居民用水实行三级阶梯水价收费如下表:
(1)若小明家去年1月份用水量20立方米,他家应缴费46元.
(2)若小明家去年2月份用水量26立方米,缴费64.4元,请求出用水在22-30立方米之间收费标准a元/立方米?
(3)在(2)的条件下,若小明家去年8月份用水量增大,共缴费87.4元,请求出他家8月份的用水量多少立方米?
| 每户每月用水量 | 水费价格(单位:元/吨) |
| 不超过20 | 2.3 |
| 超过20吨且不超过30吨的部分 | a |
| 超过30吨的部分 | 4.6 |
(2)若小明家去年2月份用水量26立方米,缴费64.4元,请求出用水在22-30立方米之间收费标准a元/立方米?
(3)在(2)的条件下,若小明家去年8月份用水量增大,共缴费87.4元,请求出他家8月份的用水量多少立方米?
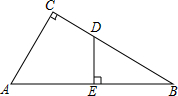 如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3.
如图,Rt△ABC中,∠C=90°,AB=10,AC=6,D是BC上一点,BD=5,DE⊥AB,垂足为E,则线段DE的长为3. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).
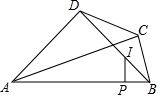 如图,Rt△ABC中,∠ACB=90°,CD为△ABC的外角平分线且∠ADB=90°.
如图,Rt△ABC中,∠ACB=90°,CD为△ABC的外角平分线且∠ADB=90°.