题目内容
9.已知:关于x的一元二次方程tx2-(3t+2)x+2t+2=0(t>0)(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1<x2),若y是关于t的函数,且y=x2-2x1,求这个函数的解析式,并画出函数图象;
(3)观察(2)中的函数图象,当y≥2t时,写出自变量t的取值范围.
分析 (1)计算判别式的值得到△=(t+2)2,从而得到△>0,所以方程有两个不相等的实数根;
(2)利用公式法解方程得到x1=1,x2=2+$\frac{2}{t}$,y=x2-2x1=$\frac{2}{t}$,然后利用描点法画函数图象;
(3)计算y=$\frac{2}{t}$与y=2t的交点,然后利用图象法写出满足y≥2t所对应的自变量的范围.
解答 (1)证明:△=9(3t+2)2-4t(2t+2)=(t+2)2,
∵t>0,
∴(t+2)2>0,即△>0,
∴方程有两个不相等的实数根;
(2)解:x=$\frac{3t+2±(t+2)}{2t}$,
∵t>0,
∴x1=1,x2=2+$\frac{2}{t}$,
∴y=x2-2x1=2+$\frac{2}{t}$-2×1=$\frac{2}{t}$,
即y=$\frac{2}{t}$(t>0);
如图,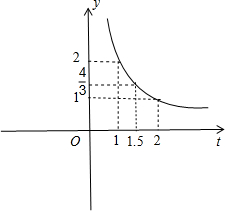
(4)当y≥2t时,0<t≤1.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了反比例函数图象.

练习册系列答案
相关题目
1.已知一次函数y=ax+b,其中x和y的部分对应值如下表:
那么方程ax+b=0的解是x=1.5.
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 7 | 5 | 3 | 1 | -1 | -3 |
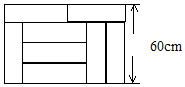 用8块相同的小长方形地砖拼成一块大长方形地面,地砖的拼放方式及相关数据如图所示,求小长方形地砖的面积.
用8块相同的小长方形地砖拼成一块大长方形地面,地砖的拼放方式及相关数据如图所示,求小长方形地砖的面积.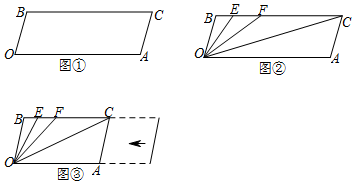
 如图,矩形ABCD的顶点A(-1,0),B(3,0),D(-1,2),CD交y轴于E;抛物线y=ax2+bx+c经过点A,B,且该抛物线的顶点为M.
如图,矩形ABCD的顶点A(-1,0),B(3,0),D(-1,2),CD交y轴于E;抛物线y=ax2+bx+c经过点A,B,且该抛物线的顶点为M.