题目内容
13.若点(2,2)在反比例函数y=$\frac{k}{x}$的图象上,则k=4,当-2<x<-1时函数值y的取值范围是-4<y<-2.分析 直接把点(2,2)代入反比例函数求出k的值即可;再分别令x=-2,x=-1求出y的对应值即可得出结论.
解答 解:∵点(2,2)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=4,
∴反比例函数的解析式为y=$\frac{4}{x}$.
∵当x=-2时,y=-2;当x=-1时,y=-4,
∴当-2<x<-1时,-4<y<-2.
故答案为:4,-4<y<-2.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
5.已知A、B在数轴上分别表示a、b.
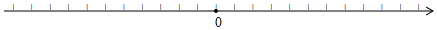
(1)对照数轴填写下表:
(2)若A、B两点间的距离记为d,试问d和a、b(a<b)有何数量关系;
(3)写出数轴上到-1和1的距离之和为2的所有整数;
(4)若点C表示的数为x,代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2,此时代数式|x+1|+|x-2|的最小值是3.
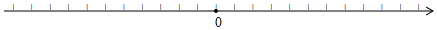
(1)对照数轴填写下表:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)写出数轴上到-1和1的距离之和为2的所有整数;
(4)若点C表示的数为x,代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2,此时代数式|x+1|+|x-2|的最小值是3.
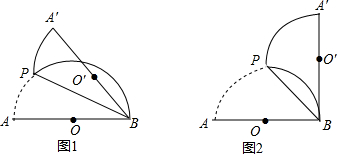
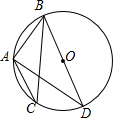 如图,BD是⊙O的直径,弦AB=AC,∠BAC=120°,已知AB=2,则AD=2$\sqrt{3}$.
如图,BD是⊙O的直径,弦AB=AC,∠BAC=120°,已知AB=2,则AD=2$\sqrt{3}$.