题目内容
3.一列火车用26秒的时间通过了一个长为256米的隧道(即从车头进入入口到车尾离开出口),又以相同的速度用了16秒的时间通过了长为96米的隧道,求这列火车的长度.若设这列火车长度为x米,则由题意可列方程为$\frac{256+x}{26}=\frac{96+x}{16}$.分析 设这列火车长度为x米,根据题意列出方程解答即可.
解答 解:设这列火车长度为x米,可得:$\frac{256+x}{26}=\frac{96+x}{16}$,
故答案为:$\frac{256+x}{26}=\frac{96+x}{16}$.
点评 此题考查一元一次方程的应用;解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
8.下列分解因式正确的是( )
| A. | a2-2b2=(a+2b)(a-2b) | B. | -x2+y2=(-x+y)(x-y) | ||
| C. | -a2+9b2=-(a+9b)(a-9b) | D. | 4x2-0.01y2=(2x+0.1y)(2x-0.1y) |
15. 如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
 如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )| A. | -2≤a≤-1 | B. | -2≤a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{2}$ | D. | -1≤a≤-$\frac{1}{4}$ |
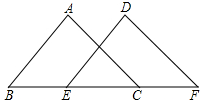 如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.