题目内容
4.如图1,AB是半圆O的直径,且AB=4,点P(不与点A、B重合)为半圆上一点.将图形沿BP折叠,分别得到点A、O的对称点A′,O′.设∠ABP=α.(1)当α=10°时,∠ABA′=20°,当点O′落在$\widehat{PB}$上时,α的度数为30°;
(2)如图2,当BA′与⊙O相切时,求折痕的长;
(3)若线段BO′与半圆只有一个公共点B,确定α的取值范围.
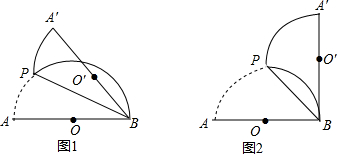
分析 (1)由折叠的性质可知∠ABA′=2∠ABP,可求得答案;当O′落在$\widehat{PB}$上时,连接OO′,则OO′⊥PB,可证得△OO′B为等边三角形,可求得答案;
(2)由切线的性质结合折叠的性质可求得∠ABP=45°,连接AP,在Rt△ABP中,由勾股定理可求得BP;
(3)由(2)可知当A′B与半圆相切时可知有一个交点,当P点向点B靠近时,则α逐渐变大,当点P与B重合时,达到最大值,可求得α的范围.
解答 解:
(1)由折叠的性质可知∠A′BP=∠ABP=α,
∴∠ABA′=2∠ABP=2α=2×10°=20°;
当O′落在$\widehat{PB}$上时,连接OO′,如图1,则OO′⊥PB,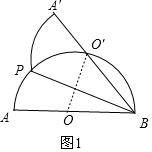
∵∠A′BP=∠ABP,
∴OB=O′B=OO′,
∴△OO′B为等边三角形,
∴∠ABA′=60°,
∴α=30°,
故答案为:20;30;
(2)当BA′与⊙O相切时,则∠ABA′=90°,
∴∠ABP=45°,
连接AP,如图2,则∠APB=90°,且AP=PB,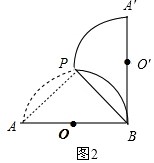
∵AB=4,
∴BP=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$,
即折痕的长为2$\sqrt{2}$;
(3)由(2)可知当A′B与半圆相切时可知有一个交点,
此时∠ABP=45°,即α=45°,
当P点向点B靠近时,则α逐渐变大,当点P与B重合时,达到最大值,
此时∠ABP=90°,
∵P与B不重合,
∴α的取值范围为:45°≤α<90.
点评 本题为圆的综合问题,涉及折叠的性质、等边三角形的判定和性质、切线的性质、等腰直角三角形、勾股定理等知识点.在(1)中的第二个空中证得△OO′B为等边三角形是解题的关键,在(2)中求得∠ABP=45°是解题的关键,在(3)中确定出满足条件的点P的两个极端位置是解题的关键.本题考查知识点较多,综合较强,难度适中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
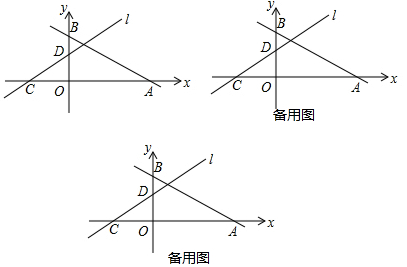
小学生10分钟应用题系列答案 如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )| A. | -2≤a≤-1 | B. | -2≤a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{2}$ | D. | -1≤a≤-$\frac{1}{4}$ |
| A. | 10cm2 | B. | 15cm2 | C. | 50cm2 | D. | 25cm2 |
| A. | $\sqrt{2}$$•\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C. | $\sqrt{8}$=4 | D. | $\sqrt{(-3)^{2}}$=-3 |
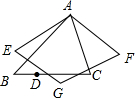 如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$.
如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,D点关于AB,AC的对称点分别是E和F,四边形AEGF是平行四边形,则四边形AEGF的面积的最小值是$\sqrt{3}$.