题目内容
7.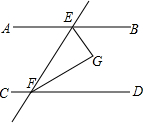 如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.
如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.(1)若∠AEF=60°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
分析 (1)先根据平行线的性质得出∠EFD=∠AEF=60°,再由FG平分∠DFE即可得出结论;
(2)先由AB∥CD得出∠BEF+∠EFD=180°,再根据EG平分∠BEF,FG平分∠DFE可得出∠GEF+∠GFE的度数,根据三角形内角和定理即可得出结论.
解答 解:(1)∵AB∥CD
∴∠EFD=∠AEF=60°,
∵FG平分∠DFE,
∵∠EFG=$\frac{1}{2}$∠DFE=$\frac{1}{2}$×60°=30°;
(2)EG⊥FG.
理由:∵AB∥CD,
∴∠BEF+∠EFD=180°,
∵EG平分∠BEF,FG平分∠DFE,
∴∠GEF=$\frac{1}{2}$∠BEF,∠GFE=$\frac{1}{2}$∠DFE,
∴∠GEF+∠GFE=$\frac{1}{2}$∠BEF+$\frac{1}{2}$∠DFE,
=$\frac{1}{2}$(∠BEF+∠DFE)
=$\frac{1}{2}$×180°
=90°,
∴∠G=180°-(∠BEF+∠DFE)=90°
∴EG⊥FG.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.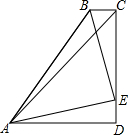 如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )
如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )
 如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )
如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )| A. | $\frac{12}{7}$ | B. | $\frac{24}{7}$ | C. | $\frac{48}{7}$ | D. | $\frac{50}{7}$ |
 在平面直角坐标系中,四边形OABC为矩形,点A的坐标为(4,0),点B的坐标为(4,3),动点M,N分别从O、B同时出发,以每秒1个单位长度的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点M作MP⊥OA,交AC于P,连接NP.下列说法①当点M运动了2秒时,点P的坐标为(2,$\frac{3}{2}$);②当点M运动$\frac{4}{3}$秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有①②③.
在平面直角坐标系中,四边形OABC为矩形,点A的坐标为(4,0),点B的坐标为(4,3),动点M,N分别从O、B同时出发,以每秒1个单位长度的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点M作MP⊥OA,交AC于P,连接NP.下列说法①当点M运动了2秒时,点P的坐标为(2,$\frac{3}{2}$);②当点M运动$\frac{4}{3}$秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有①②③. 如图在平面直角坐标系中,每个小正方形的边长为一个单位长度,将△ABC向右平移3个单位长度,再向下平移4个单位长度,得到对应的△A′B′C′.
如图在平面直角坐标系中,每个小正方形的边长为一个单位长度,将△ABC向右平移3个单位长度,再向下平移4个单位长度,得到对应的△A′B′C′.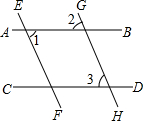 完成下面推理过程
完成下面推理过程 用尺规作图(不写作法,保留作图痕迹)
用尺规作图(不写作法,保留作图痕迹) 已知二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程x2+2x=m的解为x1=-3,x2=1.
已知二次函数y=-x2-2x+m的部分图象如图所示,则关于x的一元二次方程x2+2x=m的解为x1=-3,x2=1.