题目内容
16．
已知二次函数y=-x2-2x+m的部分图象如图所示，则关于x的一元二次方程x2+2x=m的解为x1=-3，x2=1．
分析 根据二次函数的图象得出抛物线与x轴的交点，进而可得出结论．
解答 解：∵由图可知，抛物线的对称轴为x=-1，抛物线与x轴的一个交点为-3，
∴另一个交点=2×（-1）+3=1，
∴关于x的一元二次方程x2+2x=m，即-x2-2x+m=0的解为x1=-3，x2=1．
故答案为：x1=-3，x2=1．
点评 本题考查的是抛物线与x轴的交点问题，熟知二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系是解答此题的关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
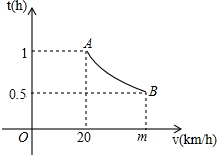一辆汽车匀速通过某段公路，所需时间t（h）与行驶速度v（km/h）满足函数关系：t=$\frac{k}{v}$，其图象为如图所示的一段曲线且端点为A（20，1）和B（m，0.5）．
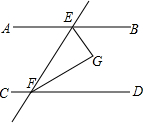如图所示，直线AB∥CD，直线AB，CD被EF所截，EG平分∠BEF，FG平分∠DFE．
8．在平面直角坐标系中，把点P（-2，3）向右平移5个单位得到点P1，再将点P1绕原点旋转90°得到点P2，则点P2的坐标是（ ）
| A． | （3，-3） | B． | （-3，3） | C． | （3，3）或（-3，-3） | D． | （3，-3）或（-3，3） |