题目内容
2.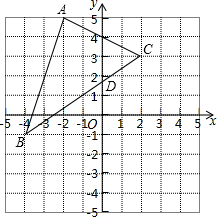 如图在平面直角坐标系中,每个小正方形的边长为一个单位长度,将△ABC向右平移3个单位长度,再向下平移4个单位长度,得到对应的△A′B′C′.
如图在平面直角坐标系中,每个小正方形的边长为一个单位长度,将△ABC向右平移3个单位长度,再向下平移4个单位长度,得到对应的△A′B′C′.(1)画出△A′B′C′并写出点B′,C′的坐标:
B′(-1,-5),C′(5,-1)
(2)试求线段BC在整个平移的过程中在坐标平面上扫过的面积.
(3)点D为BC与y轴的交点,请求出点D的坐标.
分析 (1)根据题意作出图象,即可得到B′(-1,-5),C′(5,-1);
(2)根据图形的面积的和差即可得到结论;
(3)待定系数法求得直线BC的解析式为y=$\frac{2}{3}$x+$\frac{5}{3}$,于是得到结论.
解答  解:(1)如图所示,B′(-1,-5),C′(5,-1);
解:(1)如图所示,B′(-1,-5),C′(5,-1);
故答案为:-1,-5,5,-1;
(2)由图象知,线段BC在整个平移的过程中在坐标平面上扫过的面积=9×8-$\frac{1}{2}×$4×6-$\frac{1}{2}×$3×4-$\frac{1}{2}×$4×3-$\frac{1}{2}×$6×4=36;
(3)由图象知,B(-4,-1),C(2,3),
设直线BC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-1=-4k+b}\\{3=2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=\frac{5}{3}}\end{array}\right.$,
∴直线BC的解析式为y=$\frac{2}{3}$x+$\frac{5}{3}$,
当x=0时,y=$\frac{5}{3}$,
∴D(0,$\frac{5}{3}$).
点评 本题考查了作图-平移变换,求图形的面积,直线与y轴的交点坐标,正确的作出图象是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
17.下列命题中是真命题的是( )
| A. | 线段垂直平分线上的点到这条线段的两个端点的距离相等 | |
| B. | 有两边及一角相等的两个三角形全等 | |
| C. | 一个图形和经过它旋转所得的图形中,对应的所连的线段平行且相等 | |
| D. | 对角线相等的四边形是平行四边形 |
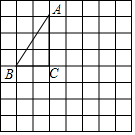 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.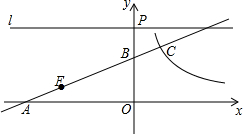 已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题:
已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题: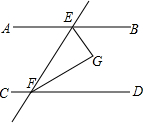 如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.
如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.