题目内容
17.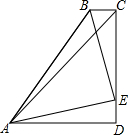 如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )
如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )| A. | $\frac{12}{7}$ | B. | $\frac{24}{7}$ | C. | $\frac{48}{7}$ | D. | $\frac{50}{7}$ |
分析 如图取CD的中点F,连接BF延长BF交AD的延长线于G,作FH⊥AB于H,EK⊥AB于K.作BT⊥AD于T.由△BCF≌△GDF,推出BC=DG,BF=FG,由△FBC≌△FBH,△FAH≌△FAD,推出BC=BH,AD=AH,由题意AD=DC=4,设BC=TD=BH=x,在Rt△ABT中,∵AB2=BT2+AT2,可得(x+4)2=42+(4-x)2,推出x=1,推出BC=BH=TD=1,AB=5,设AK=EK=y,DE=z,根据AE2=AK2+EK2=AD2+DE2,BE2=BK2+KE2=BC2+EC2,可得42+z2=2y2 ①,(5-y)2+y2=12+(4-z)2 ②,由此求出y即可解决问题.
解答 解:如图取CD的中点F,连接BF延长BF交AD的延长线于G,作FH⊥AB于H,EK⊥AB于K.作BT⊥AD于T.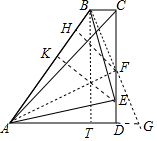
∵BC∥AG,
∴∠BCF=∠FDG,
∵∠BFC=∠DFG,FC=DF,
∴△BCF≌△GDF,
∴BC=DG,BF=FG,
∵AB=BC+AD,AG=AD+DG=AD+BC,
∴AB=AG,∵BF=FG,
∴BF⊥AF,∠ABF=∠G=∠CBF,
∵FH⊥BA,FC⊥BC,
∴FH=FC,易证△FBC≌△FBH,△FAH≌△FAD,
∴BC=BH,AD=AH,
由题意AD=DC=4,设BC=TD=BH=x,
在Rt△ABT中,∵AB2=BT2+AT2,
∴(x+4)2=42+(4-x)2,
∴x=1,
∴BC=BH=TD=1,AB=5,
设AK=EK=y,DE=z,
∵AE2=AK2+EK2=AD2+DE2,BE2=BK2+KE2=BC2+EC2,
∴42+z2=2y2 ①,
(5-y)2+y2=12+(4-z)2 ②
由②得到25-10y+2y2=5-8z+z2 ③,
①代入③可得z=$\frac{18-5y}{4}$ ④
④代入①可得y=$\frac{20}{7}$(负根已经舍弃),
∴S△ABE=$\frac{1}{2}$×5×$\frac{20}{7}$=$\frac{50}{7}$,
故选D.
点评 本题考查直角梯形的性质、全等三角形的判定和性质、角平分线的性质定理、勾股定理、二元二次方程组等知识,解题的关键是学会添加常用辅助线,学会利用参数,构建方程解决问题,属于中考压轴题.

| A. | (3x3)2=9x6 | B. | 2x3•x2=2x6 | C. | x3+x2=x5 | D. | x6÷x3=x2 |
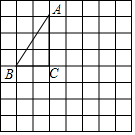 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上. 已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,求∠2,∠3的度数.
已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,求∠2,∠3的度数.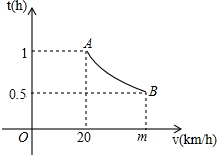 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).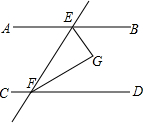 如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.
如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.