题目内容
15. 在平面直角坐标系中,四边形OABC为矩形,点A的坐标为(4,0),点B的坐标为(4,3),动点M,N分别从O、B同时出发,以每秒1个单位长度的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点M作MP⊥OA,交AC于P,连接NP.下列说法①当点M运动了2秒时,点P的坐标为(2,$\frac{3}{2}$);②当点M运动$\frac{4}{3}$秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有①②③.
在平面直角坐标系中,四边形OABC为矩形,点A的坐标为(4,0),点B的坐标为(4,3),动点M,N分别从O、B同时出发,以每秒1个单位长度的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点M作MP⊥OA,交AC于P,连接NP.下列说法①当点M运动了2秒时,点P的坐标为(2,$\frac{3}{2}$);②当点M运动$\frac{4}{3}$秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有①②③.
分析 ①正确.只要求长中线CA的解析式,求出点P坐标即可判断;
②正确.延长MP交BC于E,只要证明CE=EN,PE⊥CN即可解决问题;
③正确.根据二次函数,利用二次函数的性质即可解决问题;
解答 解:A(4,0),C(0,3),
∴直线AC的解析式为y=-$\frac{3}{4}$x+3,
当t=2时,OM=2,
∴x=2时,y=-$\frac{3}{2}$+3=$\frac{3}{2}$,
∴点P的坐标为(2,$\frac{3}{2}$),故①正确,
当t=$\frac{4}{3}$时,OM=$\frac{4}{3}$,
∵CN=4-$\frac{4}{3}$=$\frac{8}{3}$,
延长MP交BC于E,则四边形OMEC是矩形,
∴∠CEM=90°,
∴PE⊥CN,CE=OM=$\frac{4}{3}$,
∴CE=EN=$\frac{4}{3}$,
∴PC=PN,
∴△PCN是等腰三角形,故②正确,
易知S△PCN=$\frac{1}{2}$(4-t)×[3-$\frac{3}{4}$(4-t)]=-$\frac{3}{8}$(t-2)2+$\frac{3}{2}$,
∵-$\frac{3}{8}$<0,
∴t=2时,△PCN的面积最大,故③正确,
故答案为①②③
点评 本题考查矩形的性质、坐标与图形的性质、等腰三角形的判定与性质等知识,解题的关键是灵活运用所学知识解决问题,学会构建二次函数解决最值问题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
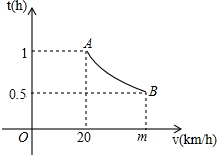 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).
 已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题:
已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题: 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点. 如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.
如图所示,直线AB∥CD,直线AB,CD被EF所截,EG平分∠BEF,FG平分∠DFE.