题目内容
13.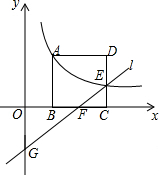 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{4}$,0).
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{4}$,0).
分析 由A(m,2)得到正方形的边长为2,则BC=2,所以n=2+m,根据反比例函数图象上点的坐标特征得到k=2•m=$\frac{2}{3}$(2+m),解得m=1,则E点坐标为(3,$\frac{2}{3}$),然后利用待定系数法确定直线GF的解析式为y=$\frac{8}{9}$x-2,再求y=0时对应自变量的值,从而得到点F的坐标.
解答 解:∵正方形的顶点A(m,2),
∴正方形的边长为2,
∴BC=2,
而点E(n,$\frac{2}{3}$),
∴n=2+m,即E点坐标为(2+m,$\frac{2}{3}$),
∴k=2•m=$\frac{2}{3}$(2+m),解得m=1,
∴E点坐标为(3,$\frac{2}{3}$),
设直线GF的解析式为y=ax+b,
把E(3,$\frac{2}{3}$),G(0,-2)代入得$\left\{\begin{array}{l}{3a+b=\frac{2}{3}}\\{b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{8}{9}}\\{b=-2}\end{array}\right.$,
∴直线GF的解析式为y=$\frac{8}{9}$x-2,
当y=0时,$\frac{8}{9}$x-2=0,解得x=$\frac{9}{4}$,
∴点F的坐标为($\frac{9}{4}$,0).
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1.某商场计划购进两种服装共100件,这两种服装的进价、售价如表所示:
(1)若商场预计进货用3500元,则这两种服装个购进多少件?
(2)若商场规定B种服装进货数量不超过A种服装进货数量的三倍,且超过A种服装进货数量的2倍,求商场有几种进货方案;
(3)在(2)条件下应该怎样进货才能使商场销售完这批货时获利最多?此时利润为多少元?
| 价格 类型 | 进价(元/件) | 售价(元/件) |
| A | 30 | 45 |
| 售价(元/部) | 50 | 70 |
(2)若商场规定B种服装进货数量不超过A种服装进货数量的三倍,且超过A种服装进货数量的2倍,求商场有几种进货方案;
(3)在(2)条件下应该怎样进货才能使商场销售完这批货时获利最多?此时利润为多少元?
3.下列运算正确的是( )
| A. | a3+a3=2a6 | B. | (x2)3=x5 | C. | 2a6÷a3=2a2 | D. | x3•x2=x5 |
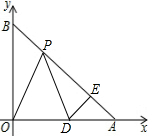 已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.