题目内容
3．直角三角形中，两直角边分别是12和5，则斜边上的中线长是6.5．分析 先根据勾股定理列式求出斜边的长，再根据直角三角形斜边上的中线等于斜边的一半解答．
解答 解：∵直角三角形中，两直角边分别是12和5，
∴斜边为$\sqrt{1{2}^{2}+{5}^{2}}$=13，
∴斜边上中线长为$\frac{1}{2}$×13=6.5．
故答案为：6.5．
点评 本题主要考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理的应用，熟记性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在线段AC、BC、CD中，线段CD最短，理由是垂线段最短．
14．如果一个角等于25°，那么它的余角是（ ）
| A． | 25° | B． | 65° | C． | 155° | D． | 75° |
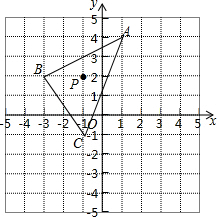如图，△ABC的三个顶点坐标分别A（1，4），B（-3，2），C（-1，-1），点P（x0，y0）为△ABC中的任意一点，经平移后点P的对应点为P1（x0+3，y0-2），将△ABC作同样的平移得到△A1B1C1
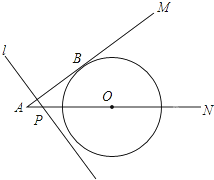如图，⊙O与射线AM相切于点B，圆心O在射线AN上，⊙O半径为6cm，OA=10cm．点P从点A出发，以2cm/秒的速度沿AN方向运动，过P点作直线l垂直AB，当l与⊙O相切时，所用时间是$\frac{5}{4}$或$\frac{35}{4}$秒．
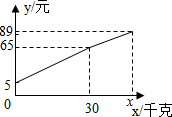一位农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用．他将土豆按市场价售出一些后，又降价出售．售出土豆的质量x（千克）与他手中持有的钱数y（元）（含备用零钱）的函数关系如图所示．结合图象回答下列问题：
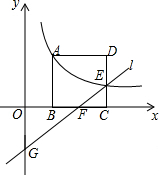如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，$\frac{2}{3}$），过点E的直线l交x轴于点F，交y轴于点G（0，-2），则点F的坐标是（$\frac{9}{4}$，0）．