题目内容

1．菱形ABCD的两条对角线相交于O，若AC=6，BD=8，则菱形ABCD的周长是（　　）
A．$4\sqrt{3}$B．20C．24D．$2\sqrt{3}$

分析 根据菱形对角线互相垂直平分的性质，可以求得BO=OD，AO=OC，在Rt△AOD中，根据勾股定理可以求得AB的长，即可求菱形ABCD的周长．

解答 解：∵菱形ABCD的两条对角线相交于O，AC=6，BD=8，由菱形对角线互相垂直平分，
∴BO=OD=4，AO=OC=3，
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5，
故菱形的周长为20，
故选：B．

点评 本题考查了勾股定理在直角三角形中的运用，以及菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键．

练习册系列答案
相关题目
11．从下列不等式中选择一个与x+1≥2组成不等式组，使该不等式组的解集为x≥1，那么这个不等式可以是（　　）
A．x＞-1B．x＞2C．x＜-1D．x＜2
12．分式方程$\frac{x+2}{x-2}$+1=$\frac{m}{x-2}$有增根，则m的值是（　　）
A．4B．3C．2D．1
9．若点P（2014，a）、Q（2015，b）都在函数y=$\frac{2016}{x}$的图象上，则下列结论中正确的是（　　）
A．a＞bB．a=b
C．a＜bD．a、b的大小关系无法确定
16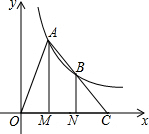．如图，点A、B在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，过点A、B作x轴的垂线，垂足分别为M，N，延长线段AB交x轴于点C，若OM=MN=NC，S△BNC=2，则k的值为（　　）
A．4B．6C．8D．12
6．若m＞n，则下列各式正确的是（　　）
A．m+4＜n+4B．6m＜6nC．-5m＜-5nD．3m-1＜3n-1
13．如图所示的△ABC中，∠ABC=90°，∠ACB=40°，AC∥BD，∠ABD=（　　）
A．40°B．50°C．140°D．130°
10．菱形ABCD的边长为4，有一个内角为120°，则较长的对角线的长为（　　）
A．4$\sqrt{3}$B．4C．$2\sqrt{3}$D．2
11．四边形ABCD中，AC⊥BD，AC≠BD，顺次连接各边中点得到的四边形是（　　）
A．正方形B．矩形C．菱形D．等腰梯形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网