题目内容
10.菱形ABCD的边长为4,有一个内角为120°,则较长的对角线的长为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
分析 利用菱形的每条对角线平分一组对角,则∠BAO=$\frac{1}{2}$∠BAD=60°,即△ABC是等边三角形,由此可求得AC=AB=4,再根据勾股定理即可求出BO的长,则BD也可求出.
解答 解:在菱形ABCD中,∠BAO=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×120°=60°,
又在△ABC中,AB=BC,
∴∠BCA=∠BAC=60°,
∠ABC=180°-∠BCA-∠BAC=60°,
∴△ABC为等边三角形,
∴AC=AB=4,
∴AO=2,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=2$\sqrt{3}$,
∴BD=2BO=4$\sqrt{3}$,
故选:A.
点评 本题主要考查的是菱形的性质:菱形的四条边都相等;对角线互相垂直平分;每条对角线平分一组对角.

练习册系列答案
相关题目
20.已知直角三角形的两直角边长分别是5和12,则此三角形的斜边长为( )
| A. | 10 | B. | 13 | C. | 15 | D. | 17 |
1. 菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
 菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )| A. | $4\sqrt{3}$ | B. | 20 | C. | 24 | D. | $2\sqrt{3}$ |
18.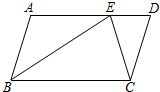 如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )
如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )
 如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )
如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )| A. | 5 | B. | 4 | C. | 3.6 | D. | 3 |
5.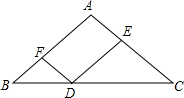 如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
 如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
15.若函数y=kx+2的图象经过点(1,3),则当y=0时,x=( )
| A. | -2 | B. | 2 | C. | 0 | D. | ±2 |
2.在-2,+3.5,0,$\frac{2}{3}$,-0.7,11中,负数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.下列说法正确的是( )
| A. | -2是4的平方根 | B. | 4的平方根是2 | C. | 2没有平方根 | D. | $\root{3}{3}$大于$\frac{3}{2}$ |
20.为了了解某县七年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法正确的是( )
| A. | 9800名学生是总体 | B. | 每个学生是个体 | ||
| C. | 100名学生是所抽取的一个样本 | D. | 样本容量是100 |