题目内容
11.四边形ABCD中,AC⊥BD,AC≠BD,顺次连接各边中点得到的四边形是( )| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 等腰梯形 |
分析 此题要根据矩形的性质和三角形中位线定理求解;首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若原四边形的对角线必互相垂直,则所得四边形是矩形.
解答  解:∵点E、F分别为AB、BC的中点,
解:∵点E、F分别为AB、BC的中点,
∴EF∥AC;同理可证FG∥BD.
∴四边形EFGH是平行四边形.
又∵AC⊥BD,
∴EF⊥FG,即∠EFG=90°,
∵四边形EFGH为矩形,
故选:B.
点评 本题主要考查了矩形的性质和三角形中位线定理,解题的关键是构造三角形利用三角形的中位线定理解答.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1. 菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
 菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )| A. | $4\sqrt{3}$ | B. | 20 | C. | 24 | D. | $2\sqrt{3}$ |
2.在-2,+3.5,0,$\frac{2}{3}$,-0.7,11中,负数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.下列说法正确的是( )
| A. | -2是4的平方根 | B. | 4的平方根是2 | C. | 2没有平方根 | D. | $\root{3}{3}$大于$\frac{3}{2}$ |
6. 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )| A. | OA=OC,OB=OD | B. | AB=CD,AO=CO | C. | AD∥BC,AD=BC | D. | ∠BAD=∠BCD,AB∥CD |
16.某反比例函数的图象经过点(-2,3),则该图象一定不经过点( )
| A. | (1,6) | B. | (-1,6) | C. | (2,-3) | D. | (3,-2) |
3. 如图是某班50名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
如图是某班50名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
 如图是某班50名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
如图是某班50名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )| A. | 5-10元 | B. | 10-15元 | C. | 15-20元 | D. | 20-25元 |
20.为了了解某县七年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法正确的是( )
| A. | 9800名学生是总体 | B. | 每个学生是个体 | ||
| C. | 100名学生是所抽取的一个样本 | D. | 样本容量是100 |
12.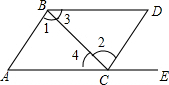 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )| A. | ∠3=∠4 | B. | ∠D=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠ACD=180° |