题目内容
14.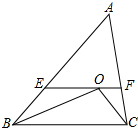 如图,△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC交AB、AC于E、F,若△ABC的周长比△AEF的周长大12cm,O到AB的距离为3cm,△OBC的面积18cm2.
如图,△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC交AB、AC于E、F,若△ABC的周长比△AEF的周长大12cm,O到AB的距离为3cm,△OBC的面积18cm2.
分析 根据角平分线定义和平行线性质求出∠EOB=∠EBO,∠FCO=∠FOC,根据等腰三角形的判定得出OE=BE,OF=FC,求出BC长,根据三角形的面积公式求出即可.
解答 解:∵∠B与∠C的平分线交于点O,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FCO=∠FOC,
∴OE=BE,OF=FC,
∴EF=BE+CF,
∴AE+EF+AF=AB+AC,
∵△ABC的周长比△AEF的周长大12cm,
∴(AC+BC+AC)-(AE+EF+AF)=12,
∴BC=12cm,
∵O到AB的距离为3cm,
∴△OBC的面积是$\frac{1}{2}×12$cm×3cm=18cm2.,
故答案为:18.
点评 本题考查了平行线的性质,等腰三角形的判定,角平分线定义,三角形的面积的应用,能求出EF=BE+CF是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.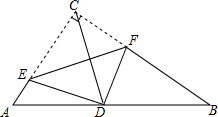 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )
 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,翻折∠C,使点C落在边AB的中点D处,折痕为EF(E、F分别在边AC、BC上),则EF的长为( )| A. | $\frac{5}{2}$ | B. | $\frac{15}{4}$ | C. | $\frac{116}{35}$ | D. | $\frac{125}{48}$ |
2.下列说法中,正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 有一组邻边相等的平行四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
19.一元二次方程x2+1=0的根是( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 无实数根 |
6. 如图所示,下列的图形旋转一周形成左边图形形状的是( )
如图所示,下列的图形旋转一周形成左边图形形状的是( )
 如图所示,下列的图形旋转一周形成左边图形形状的是( )
如图所示,下列的图形旋转一周形成左边图形形状的是( )| A. |  | B. |  | C. |  | D. |  |
4.抛物线y=ax2+bx+c经过点A(-1,2),B(1,-2),则b的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |