抛物线y=ax2+bx+c经过点A.则b的值为( )A．2B．-2C．4D．-4 题目和参考答案——青夏教育精英家教网—

题目内容

4．抛物线y=ax²+bx+c经过点A（-1，2），B（1，-2），则b的值为（　　）

A．

B．

-2

C．

D．

-4

分析根据二次函数图象上点的坐标特征，把点A和点B的坐标分别代入解析式得到a-b+c=2，a+b+c=-2，然后把两式相减即可得到b的值．

解答解：∵点A（-1，2），B（1，-2）在抛物线y=ax²+bx+c上，
∴$\left\{\begin{array}{l}{a-b+c=2①}\\{a+b+c=-2②}\end{array}\right.$，
②-①得2b=-4，
∴b=-2．
故选B．

点评本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．

练习册系列答案

相关题目

14．

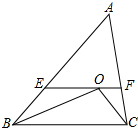如图，△ABC中，∠B与∠C的平分线交于点O，过O作EF∥BC交AB、AC于E、F，若△ABC的周长比△AEF的周长大12cm，O到AB的距离为3cm，△OBC的面积18cm²．

a³+a³=a⁶

（a³）²=a⁶

a⁸÷a⁴=a²

12．已知某抛物线是由抛物线y=ax²向上平移3个单位长度得到的，且该抛物线过点（1，0）．求其函数的解析式．

19．我国铁路实现了第六次大提速，给旅客的出行带来了很大的方便．例如，京沪线全长约1500公里，第六次提速后，特快列车运行全程所用时间比第五次提速后少用1$\frac{7}{8}$小时．已知第六次提速后与第五次提速后的平均时速比为5：4．求第五次提速后和第六次提速后的平均时速各是多少？

9．若△ABC∽△A′B′C′，且相似比为3：5，已知△ABC的周长为21，则△A′B′C′的周长为25．

16．数轴上两点A、B分别表示实数$\sqrt{19}$和4．
（1）请判断A、B两点的位置，即点A在点B的左边还是右边？
（2）计算A、B两点之间的距离（精确到0.01）

13．已知a+b=1，则式子9-a-b的值是（　　）

20．设a、b是方程x²+3x+1=0的两实根，则代数式$\frac{1}{a^2}+\frac{1}{b^2}$的值为（　　）

试题分类