题目内容
4.关于x的不等式组$\left\{\begin{array}{l}{\frac{x+5}{2}>x-3,①}\\{\frac{2x+2}{3}<x+a,②}\end{array}\right.$只有4个整数解,求a的取值范围.分析 首先利用不等式的基本性质解不等式组,再从不等式的解集中找出适合条件的整数解,再确定字母的取值范围即可.
解答 解:$\left\{\begin{array}{l}{\frac{x+5}{2}>x-3,①}\\{\frac{2x+2}{3}<x+a,②}\end{array}\right.$
由①得:x<11,
由②得:x>2-3a,
不等式组的解集为:2-3a<x<11
∵不等式组只有4个整数解为10、9、8、7
∴6≤2-3a<7
∴-$\frac{5}{3}$<a≤-$\frac{4}{3}$.
点评 本题考查了一元一次不等式组的解法,由x的特殊解求a的取值范围是解决此类题型常用的思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知x2+2mx+16是完全平方式,则m的值是( )
| A. | ±4 | B. | 4 | C. | -4 | D. | ±8 |
 如图,已知a、b、c在数轴上的位置,化简:|a-b|-|b-c|+|c-a|=2b-2a.
如图,已知a、b、c在数轴上的位置,化简:|a-b|-|b-c|+|c-a|=2b-2a.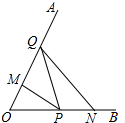
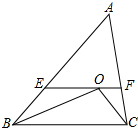 如图,△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC交AB、AC于E、F,若△ABC的周长比△AEF的周长大12cm,O到AB的距离为3cm,△OBC的面积18cm2.
如图,△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC交AB、AC于E、F,若△ABC的周长比△AEF的周长大12cm,O到AB的距离为3cm,△OBC的面积18cm2.