题目内容
8.某中学展开了“保护环境,绿化校园”主题月活动,在校团委的倡议下,全校师生共捐款4363元用于购买桂花树和丁香树绿化校园.(1)若购买5棵桂花树和4棵丁香树需花费410元,购买3棵桂花树和2棵丁香树需花费230元,求桂花树和丁香树的单价;
(2)按校团委规划,准备购买桂花树和丁香树共100棵,且购买桂花树的数量不少于34棵,请你分析有哪几种购买方案.
分析 (1)设桂花树的单价为x元,丁香树的单价位y元,根据购买5棵桂花树和4棵丁香树需花费410元,购买3棵桂花树和2棵丁香树需花费230元可列方程组求解;
(2)设购买购买a棵桂花树,则购买丁香树(100-a)棵,根据总费用不超过4363元,进而得出a的取值范围,进而得出答案.
解答 解:(1)设桂花树的单价为x元,丁香树的单价位y元,由题意可得,
$\left\{\begin{array}{l}{5x+4y=410}\\{3x+2y=230}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=40}\end{array}\right.$,
答:桂花树的单价为50元,丁香树的单价位40元;
(2)设购买a棵桂花树,由题意可得:
50a+40(100-a)≤4363,
解得:a≤36.3,
∵a≥34,且a为正整数,
∴a=34,35,36,
∴共有3种方案,
方案一:购买桂花树34棵,丁香树66棵;
方案二:购买桂花树35棵,丁香树65棵;
方案三:购买桂花树36棵,丁香树64棵.
点评 本题考查一元一次方程的应用,一元一次不等式组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的关系列出方程或不等式组,再求解.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
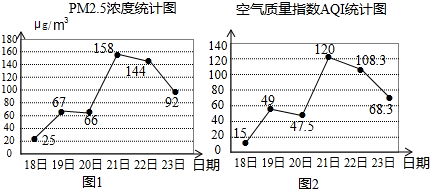
18.如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”),由图可得下列说法:①18日的PM2.5浓度最低;
②这六天中PM2.5浓度的中位数是112μg/m3;
③这六天中有4天空气质量为“优良”;
④空气质量指数AQI与PM2.5浓度有关.
其中正确的是( )
②这六天中PM2.5浓度的中位数是112μg/m3;
③这六天中有4天空气质量为“优良”;
④空气质量指数AQI与PM2.5浓度有关.
其中正确的是( )

| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
13.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{0.5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{12}$ |
 如图,双曲线y=$\frac{2}{x}$(x>0),y=$\frac{12}{x}$(x>0),P、Q为y轴正半轴上两点,设P点的坐标为(0,a-2),PQ=4,分别过P、Q两点作x轴的平行线交两支曲线于C、D、A、B(如图)
如图,双曲线y=$\frac{2}{x}$(x>0),y=$\frac{12}{x}$(x>0),P、Q为y轴正半轴上两点,设P点的坐标为(0,a-2),PQ=4,分别过P、Q两点作x轴的平行线交两支曲线于C、D、A、B(如图)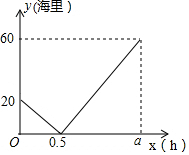 在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.
在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示. 已知,如图,在△ABC中,∠ACB=90°,AB=5cm,BC=4cm,CD⊥AB于D,求CD的长.
已知,如图,在△ABC中,∠ACB=90°,AB=5cm,BC=4cm,CD⊥AB于D,求CD的长.