题目内容
17.某学校为了庆祝国庆节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花共需13元;2盆A种花和1盆B种花共需11元.(1)求1盆A种花和1盆B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
分析 (1)1盆A种花的售价为x元,1盆B种花的售价是y元,根据:“1盆A种花和2盆B种花共需13元;2盆A种花和1盆B种花共需11元”列方程组求解即可;
(2)首先根据“A种盆花的数量不超过B种盆花数量的2倍”确定m的取值范围,然后得出最值即可.
解答 解:(1)1盆A种花的售价为x元,1盆B种花的售价是y元,根据题意可得:
$\left\{\begin{array}{l}{x+2y=13}\\{2x+y=11}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$,
答:1盆A种花的售价为3元,1盆B种花的售价是5元;
(2)设购进A种花m盆,依据题意可得:
m≤2(100-m)
解得:m≤66$\frac{2}{3}$,而m为正整数,
∴m最多=66,
答:A种盆花最多购进66盆.
点评 此题主要考查了二元一次方程组的应用以及一次函数的应用等知识,根据题意得出正确的等量关系是解题关键.

练习册系列答案
相关题目
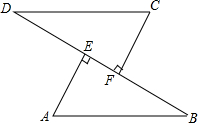 如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD.
如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD.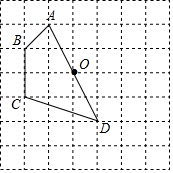 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题:
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题: 如图,A、B、C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭P,使景点B、景点C到凉亭P的距离之和等于景点B到景点A的距离,请用直尺和圆规在所给的图中作出点P.(不写作法和证明,只保留作图痕迹)
如图,A、B、C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭P,使景点B、景点C到凉亭P的距离之和等于景点B到景点A的距离,请用直尺和圆规在所给的图中作出点P.(不写作法和证明,只保留作图痕迹)



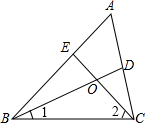 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.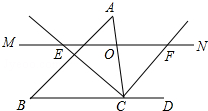 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.