题目内容
18．
已知，如图，在△ABC中，∠ACB=90°，AB=5cm，BC=4cm，CD⊥AB于D，求CD的长．
分析 根据勾股定理求出AC，根据三角形的面积公式计算即可．
解答 解：由勾股定理得，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=3cm，
∵∠ACB=90°，CD⊥AB，
∴$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×CD，即3×4=5×CD，
解得，CD=$\frac{12}{5}$cm．
点评 本题考查的是勾股定理的应用，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
相关题目
请从以下两个小题中任选一个作答，若多选，则按第一题计分．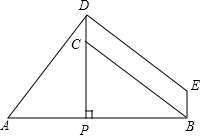
如图，点P在线段AB上，PD⊥AB，点C在线段PD上，连结BC，以CB，CD为邻边构造□BCDE，若AD=DE，AP=PC．
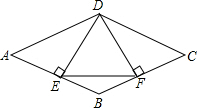如图，在菱形ABCD中，过点D作DE⊥AB于点E，作DF⊥BC于点F，连接EF．
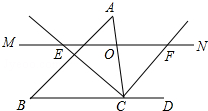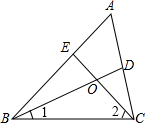
如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．