题目内容
18. 如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
分析 根据二次函数的性质,平移过程中扫过的面积等于平行四边形的面积,然后列方程求出OA,从而得到点A的坐标,再代入抛物线解析式求解即可.
解答  解:如图,抛物线上A、B两点间的部分在平移过程中扫过的面积等于?ABOC的面积,
解:如图,抛物线上A、B两点间的部分在平移过程中扫过的面积等于?ABOC的面积,
∵平移过程中扫过的面积为9,
∴3•OA=9,
解得OA=3,
∴点A的坐标为(3,0),
代入得a•32+2×3+3=0,
解得a=-1.
故答案为:-1.
点评 本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,理解并判断出平移扫过的面积等于平行四边形的面积是解题的关键.

练习册系列答案
相关题目
13.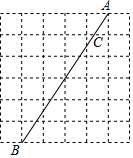 如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为点C,则AC:CB为( )
如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为点C,则AC:CB为( )
 如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为点C,则AC:CB为( )
如图,在6×6的正方形网格中,连接两格点A,B,线段AB与网格线的交点为点C,则AC:CB为( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
3.从分别写有数字-4、-3、-2、-1、0、1、2、3、4的九张一样的卡片中,任意抽取一张卡片,则所抽卡片上数字的绝对值小于2<“m“:math xmlns:dsi='http://www.dessci.com/uri/2003/MathML'dsi:zoomscale='150'dsi:_mathzoomed='1'style='CURSOR:pointer; DISPLAY:inline-block'>2$\sqrt{2}$的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
7.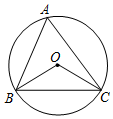 如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )
如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )
 如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )
如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠BAC=60°,则BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
8. 如图所示几何体的主视图为( )
如图所示几何体的主视图为( )
 如图所示几何体的主视图为( )
如图所示几何体的主视图为( )| A. |  | B. |  | C. |  | D. |  |
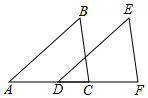 在△ABC和△DEF中,A、D、C、F在同一条直线上,且AB=DE,AD=CF,另外只能再在给出的三个条件:①∠B=∠E;②AB∥DE;③∠ACB=∠DFE中选择其中一个用来证明△ABC与△DEF全等,这个条件应该是②(填写编号),并证明△ABC≌△DEF.
在△ABC和△DEF中,A、D、C、F在同一条直线上,且AB=DE,AD=CF,另外只能再在给出的三个条件:①∠B=∠E;②AB∥DE;③∠ACB=∠DFE中选择其中一个用来证明△ABC与△DEF全等,这个条件应该是②(填写编号),并证明△ABC≌△DEF. 如图,AB=AC,BD=CD,若∠B=30°,∠BDC=100°,则∠A=40°.
如图,AB=AC,BD=CD,若∠B=30°,∠BDC=100°,则∠A=40°. 如图,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.
如图,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.