题目内容
10. 如图,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.
如图,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.
分析 根据圆周角定理可得出∠AOB的度数,再由OA=OB,可求出∠ABO的度数.
解答 解:由题意得,∠AOB=2(∠ADC+∠BAC)=80°,
∵OA=OB(都是半径),
∴∠ABO=∠OAB=$\frac{1}{2}$(180°-∠AOB)=50°.
故答案为:50°.
点评 本题考查了圆周角定理,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
18. 如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
 如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
5.在我市开展的“好书伴我成长”读书活动中,学校随机调查了九年级50名学生度数的册数统计数据如下表所示:
那么这50名学生读书册数的平均数与中位数分别为( )
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
| A. | 2和3 | B. | 3和3 | C. | 2和2 | D. | 3和2 |
15.如果点A(m,n)、B(m-1,n-2)均在一次函数y=kx+b(k≠0)的图象上,那么k的值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
2.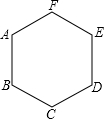 如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
 如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )| A. | $5\sqrt{2}$cm | B. | $5{\sqrt{3}^{\;}}$cm | C. | 5(1+$\sqrt{2}$)cm | D. | 5(1+$\sqrt{3}$)cm |
19.函数y=$\frac{k}{x}$的图象经过点A(1,-5),则k的值为( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
 如图,在梯形ABCD中,AB∥CD,AD=BC=4,CD=2,AB=6,DM⊥AB,垂足为M,CN⊥AB,垂足为N,点P、Q分别是线段DM、CN上的动点,且DP=NQ,顺次联结AP、PQ、QB,设DP=t.
如图,在梯形ABCD中,AB∥CD,AD=BC=4,CD=2,AB=6,DM⊥AB,垂足为M,CN⊥AB,垂足为N,点P、Q分别是线段DM、CN上的动点,且DP=NQ,顺次联结AP、PQ、QB,设DP=t. 如图,E是线段AD上一点,AB=AC,BE=CE,求证:
如图,E是线段AD上一点,AB=AC,BE=CE,求证: