题目内容
6. 如图,AB=AC,BD=CD,若∠B=30°,∠BDC=100°,则∠A=40°.
如图,AB=AC,BD=CD,若∠B=30°,∠BDC=100°,则∠A=40°.
分析 根据SSS证△BAD≌△CAD,根据全等得出∠BAD=∠CAD,∠B=∠C=30°,根据三角形的外角性质得出∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,求出∠BDC=∠B+∠C+∠BAC,代入求出即可.
解答 解:过D作射线AF,
在△BAD和△CAD中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=DC}\end{array}\right.$,
∴△BAD≌△CAD(SSS),
∴∠BAD=∠CAD,∠B=∠C=30°,
∵∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD,
∴∠BDC=∠B+∠C+∠BAC,
∵∠C=∠B=30°,∠BDC=100°,
∴∠BAC=40°,
故答案为40°.
点评 本题考查了全等三角形的性质和判定,三角形的外角性质的应用,解此题的关键是求出∠BDC=∠B+∠C+∠BAC和∠C的度数,难度适中.

练习册系列答案
相关题目
18. 如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
 如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为-1.
15.如果点A(m,n)、B(m-1,n-2)均在一次函数y=kx+b(k≠0)的图象上,那么k的值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
16.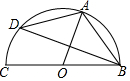 如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
 如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
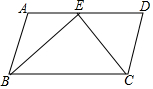 如图.已知四边形ABCD为平行四边形,AD=2AB,E为AD的中点,试说明BE与EC的位置关系.并说明理由.
如图.已知四边形ABCD为平行四边形,AD=2AB,E为AD的中点,试说明BE与EC的位置关系.并说明理由.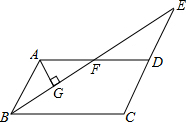 如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点.
如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点. 如图,E是线段AD上一点,AB=AC,BE=CE,求证:
如图,E是线段AD上一点,AB=AC,BE=CE,求证: