题目内容
4.小明准备用一段长40米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.(1)请用a表示第三条边长.
(2)求出a的取值范围.
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说出你的围法;若不能,请说明理由.
分析 (1)本题需先表示出第二条边长,即可得出第三条边长.
(2)本题需先求出三边的长,再根据三角形的三边关系列出不等式组,即可求出a的取值范围.
(3)本题需先求出a的值,然后即可得出三角形的三边长.
解答 解:(1)∵第二条边长为2a+2,
∴第三条边长为40-a-(2a+2)=38-3a.
(2)根据题意得:
$\left\{\begin{array}{l}{a+2a+2>38-3a}\\{a+38-3a>2a+2}\\{2a+2+38-3a>a}\end{array}\right.$,
解得:6<a<9.
则a的取值范围是:6<a<9.
(3)在(2)的条件下,注意到a为整数,所以a只能取7或8.
当a=7时,三角形的三边长分别为7,16,17.由72+162≠172知,此时不能构成直角三角形.
当a=8时,三角形的三边长分别为8,18,14.由82+142≠182知,恰此时不能构成直角三角形.
综上所述,不能围成满足条件的小圈是直角三角形形状.
点评 本题主要考查了一元一次不等式组的应用,在解题时要能根据三角形的三边关系,列出不等式组是本题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
16. 如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( )
 如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( )| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
 如图,小强和小红一起搭积木,小强所搭的“小塔”高度为23cm,小红所搭的“小树”高度为22cm,求每块A、B型积木的高度.
如图,小强和小红一起搭积木,小强所搭的“小塔”高度为23cm,小红所搭的“小树”高度为22cm,求每块A、B型积木的高度. 某种品牌牛奶包装盒的表面展开图如图所示(单位:mm),那么这种牛奶包装盒的容积是2.24×105mm3(包装材料厚度不计).
某种品牌牛奶包装盒的表面展开图如图所示(单位:mm),那么这种牛奶包装盒的容积是2.24×105mm3(包装材料厚度不计).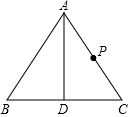 如图,等边三角形ABC,D为BC边的中点,AD=12,P为AC的中点,问在AD是否存在一点Q,使CQ+PQ最小,如果存在,写出作图思路,画出Q的位置,并求出这个最小值;如果不存在,说明理由.
如图,等边三角形ABC,D为BC边的中点,AD=12,P为AC的中点,问在AD是否存在一点Q,使CQ+PQ最小,如果存在,写出作图思路,画出Q的位置,并求出这个最小值;如果不存在,说明理由.