题目内容
14．
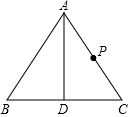如图，等边三角形ABC，D为BC边的中点，AD=12，P为AC的中点，问在AD是否存在一点Q，使CQ+PQ最小，如果存在，写出作图思路，画出Q的位置，并求出这个最小值；如果不存在，说明理由．
分析 存在．如图，连接PB交AD于点Q，此时QP+CQ的值最小．根据等边三角形的性质，等边三角形的两条中线相等．
解答 解：存在．如图，连接PB交AD于点Q，此时QP+CQ的值最小．
∵△ABC是等边三角形，BD=CD，
∴QB=QC，
∴CQ+PQ=BP+PQ=PB，
∵AP=PC，BD=CD，
∴AD、BP是△ABC的中线，且AD=BP=12．
∴CQ+PQ的最小值为12．
点评 本题考查轴对称-最短问题、垂线段最短、等边三角形的性质等知识，解题的关键是学会利用对称解决最短问题，属于中考常考题型．
练习册系列答案
相关题目
2．将两个斜边长相等的三角形纸片如图①放置，其中∠ACB=∠CED=90°，∠A=45°，∠D=30°．把△DCE绕点C顺时针旋转15°得到△D1CE1，如图②，连接D1B，则∠E1D1B的度数为（ ）
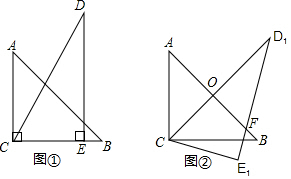
| A． | 10° | B． | 15° | C． | 7.5° | D． | 20° |
9．若y=（3+m）x${\;}^{{m}^{2}-9}$是开口向下的抛物线，则m的值（ ）
| A． | 3 | B． | -3 | C． | $\sqrt{11}$ | D． | -$\sqrt{11}$ |
4．已知在△ABC中∠A=40°，∠B=50°，则△ABC为（ ）
| A． | 锐角三角形 | B． | 钝角三角形 | C． | 直角三角形 | D． | 以上都有可能 |