题目内容
17.根据已知条件确定二次函数的表达式(1)图象的顶点为(2,3),且经过点(3,6)
(2)二次函数y=ax2+bx+c的对称轴为x=3,最小值为-2,且过(0,1),求此函数的解析式.
(3)图象经过点(1,0),(0,-3),且对称轴是直线x=2.
分析 (1)根据抛物线的顶点坐标设出,抛物线的解析式为:y=a(x-2)2+3,再把(3,6)代入,求出a的值,即可得出二次函数的解析式;
(2)设顶点式为y=a(x-3)2-2,然后把(0,1)代入求出a即可;
(3)根据题意设出抛物线的解析式为y=a(x-2)2+k.把A(1,0),B(0,-3)的坐标代入,利用待定系数法求得即可.
解答 解:(1)∵图象的顶点为(2,3),且经过点(3,6),
设抛物线的解析式为:y=a(x-2)2+3,再把(3,6)代入,
可得a(3-2)2+3=6,
∴a=3,
∴抛物线的解析式为:y=3(x-2)2+3;
(2)设抛物线解析式为y=a(x-3)2-2,
把(0,1)代入得9a-2=1,解得a=$\frac{1}{3}$,
所以抛物线解析式为y=$\frac{1}{3}$(x-3)2-2;
(3)设抛物线的解析式为y=a(x-2)2+k.把A(1,0),B(0,-3)的坐标代入,得
$\left\{\begin{array}{l}{0={a(1-2)}^{2}+k}\\{-3={a(0-2)}^{2}+k}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-1}\\{k=1}\end{array}\right.$
∴y=-(x-2)2+1=-x2+4x-3.
即这个二次函数的解析式为y=-x2+4x-3.
点评 本题主要考查了待定系数法求解析式,二次函数的解析式有三种常见形式:①一般式:y=ax2+bx+c(a,b,c是常数,a≠0); ②顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标; ③交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0);熟练掌握并运用以上三种解析式是解答此题的关键.

 阅读快车系列答案
阅读快车系列答案| 住院或重疾门诊费用 | 报销比例 |
| 1000元以下(含1000元)部分 | 50% |
| 1000元至5000元(含5000元)部分 | 60% |
| 5000元至10000元(含10000元)部分 | 70% |
| 10000元至30000元(含30000元)部分 | 80% |
| 30000元以上部分 | 90% |
(1)分别计算当住院费用为1000元和5000元时,可报销的费用为多少?
(2)若某校学生小宇因病住院,出院后报销的费用为3050元,求小宇的住院费用;
(3)当住院费用为多少时,患者本人恰好承担住院费用的$\frac{1}{3}$?
 如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$在第二象限交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{3}$.
如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$在第二象限交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{3}$. 甲、乙两人从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的关系的图象如图所示.根据图中提供的信息,有下列说法:
甲、乙两人从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的关系的图象如图所示.根据图中提供的信息,有下列说法: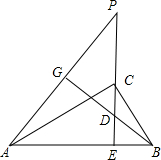 如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE.
如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE.