题目内容
16. 如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( )| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
分析 设AC=x,则BD=12-x,根据题意表示出四边形ABCD的面积,根据二次函数的性质解答.
解答 解:设AC=x,则BD=12-x,
则四边形ABCD的面积=$\frac{1}{2}$AC×BD=$\frac{1}{2}$×x×(12-x)=-$\frac{1}{2}$x2+6x=-$\frac{1}{2}$(x-6)2+18,
∴当x=6时,四边形ABCD的面积最大,最大值是18,
故选:B.
点评 本题考查的是三角形的面积计算,掌握二次函数的性质、四边形的面积公式是解题的关键.

练习册系列答案
相关题目
1.学校采购了15块泡沫板用于科技制作,每块规格为10dm×10dm,现按要求用这些材料制成10个同样大小的正方体盒子(材料没有剩余),则盒子的棱长为( )
| A. | 5dm | B. | 6dm | C. | 7dm | D. | 15dm |
8.下面现象能说明“面动成体”的是( )
| A. | 旋转一扇门,门运动的痕迹 | |
| B. | 扔一块小石子,小石子在空中飞行的路线 | |
| C. | 天空划过一道流星 | |
| D. | 时钟秒针旋转时扫过的痕迹 |
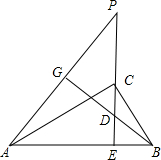 如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE.
如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE.