题目内容
11.已知圆锥的轴截面为等边三角形,则(1)圆锥的侧面展开图的圆心角度数为180°;(2)圆锥的侧面积与底面积之比为2:1.分析 如图,设等边△ABC的边长为2a,则圆锥的母线长为2a,底面圆的半径为a,设圆锥的侧面展开图的圆心角度数为n°,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到$\frac{n•π•2a}{180}$=2πa,解方程求出n即可得到圆锥的侧面展开图的圆心角度数;然后计算圆锥的侧面积和底面积,再计算它们的比.
解答 解:如图,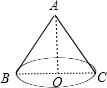 设等边△ABC的边长为2a,则圆锥的母线长为2a,底面圆的半径为a,
设等边△ABC的边长为2a,则圆锥的母线长为2a,底面圆的半径为a,
设圆锥的侧面展开图的圆心角度数为n°,
则$\frac{n•π•2a}{180}$=2πa,解得n=180,
即圆锥的侧面展开图的圆心角度数为180°;
圆锥的侧面积=$\frac{1}{2}$•2πa•2a=2πa2,底面积=πa2,
所以圆锥的侧面积与底面积之比=2πa2:πa2=2:1.
故答案为180°,2:1.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
3.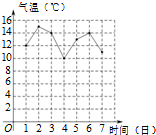 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )| A. | 13,13 | B. | 14,14 | C. | 13,14 | D. | 14,13 |
20.从2015年秋季学期起,北京110 000名初一新生通过“北京市初中实践活动管理服务平台”进行选课,参加“开放性科学实践活动”课程.将110 000用科学记数法表示应为( )
| A. | 11×104 | B. | 1.1×105 | C. | 1.1×106 | D. | 0.11×106 |
 如图,?ABCD中,AB=2cm,AC=5cm,S?ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.
如图,?ABCD中,AB=2cm,AC=5cm,S?ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.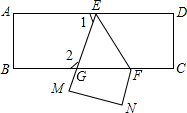 如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.
如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数. 如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE,AE交⊙O于点F.
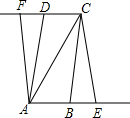
如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE,AE交⊙O于点F.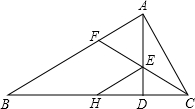 如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.
如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.