题目内容
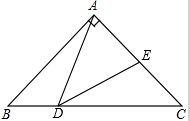 已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为
已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为考点:相似三角形的判定与性质
专题:
分析:分两种情况,当∠ADE为顶角时,可证明△ABD≌△DCE,可求得CE;当∠ADE为底角时,则只有EA=ED,根据条件可知∠DAE=45°,可知E为AC中点,可求得CE.
解答:解:
当∠ADE为顶角时,则有DA=DE,
∵AB=AC=2,∠BAC=90°,
∴∠C=∠B=45°,
∵∠ADE=45°,
∴∠ADC=45°+∠EDC,
又∠ADC=∠B+∠BAD=45°+∠BAD,
∴∠BAD=∠EDC,
在△ABD和△DCE中
∴△ABD≌△DCE(AAS),
∴CD=AB=2,CE=BD,
在Rt△ABC中,AB=AC=2,可求得BC=2
,
∴CE=BD=BC-CD=2
-2;
当∠ADE为底角时,则只有AE=DE,可知∠DAE=45°,∠DEA=90°,
∴E为AC的中点,
∴CE=1,
综上可知CE的长为1或2
-2,
故答案为:1或2
-2.
当∠ADE为顶角时,则有DA=DE,
∵AB=AC=2,∠BAC=90°,
∴∠C=∠B=45°,
∵∠ADE=45°,
∴∠ADC=45°+∠EDC,
又∠ADC=∠B+∠BAD=45°+∠BAD,
∴∠BAD=∠EDC,
在△ABD和△DCE中
|
∴△ABD≌△DCE(AAS),
∴CD=AB=2,CE=BD,
在Rt△ABC中,AB=AC=2,可求得BC=2
| 2 |
∴CE=BD=BC-CD=2
| 2 |
当∠ADE为底角时,则只有AE=DE,可知∠DAE=45°,∠DEA=90°,
∴E为AC的中点,
∴CE=1,
综上可知CE的长为1或2
| 2 |
故答案为:1或2
| 2 |
点评:本题主要考查等腰三角形的性质和全等三角形的判定和性质,根据条件确定出E点的位置是解题的关键,注意结合勾股定理、直角三角形的性质.

练习册系列答案
相关题目
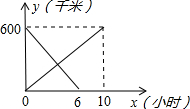 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时,出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
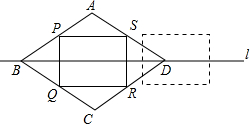 在菱形ABCD中,AB=5cm,BD=8cm,P,Q,R,S分别是菱形各边的中点.将长方形PQRS沿着直线L向右移动5cm,则长方形PQRS与菱形ABCD重叠的面积是多少?
在菱形ABCD中,AB=5cm,BD=8cm,P,Q,R,S分别是菱形各边的中点.将长方形PQRS沿着直线L向右移动5cm,则长方形PQRS与菱形ABCD重叠的面积是多少? 如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.
如图,已知圆的直径,AB=6cm,CD是圆上长为2cm的弦,当弦CD在半圆AB上滑动时,AC和BD延长线的夹角是否为定值?如果不是,说明理由;如果是,求出这个定角的正弦值.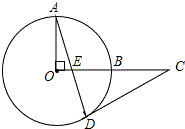 如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连接AD交OB于点E.求证:CD=CE.
如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连接AD交OB于点E.求证:CD=CE.