题目内容
某品牌装卖店准备销售男女两款T恤,进价都是30元,并以相同的销售价x(元)进行销售,其中50≤x≤120.经市场调查发现:女款T恤的定价为50元时,月销售量为120件;售价不超过90元时,价格每上涨1元,销售量减少1件;销售价不低于90元时,超过90元的部分每上涨1元,销售量减少2件;设该品牌专卖店销售女款T恤的月利润为y1(元),销售男款T恤月利润为y2(元),销售这两款T恤的月利润总和为y(元).
(1)当x=90时,女款T恤的月销量为 件;?
当50≤x≤90时?女款T恤的月销量为 件(用含x的代数式表示);?
当90≤x≤120时?女款T恤的月销量为 件(用含x的代数式表示);
(2)若女款T恤的月销售量为100件,售价为多少元?
(3)求y1与x的函数关系式;
(4)若男款T恤月利润y2与x的函数关系式为:y2=20x+3000,求销售这款T恤的月销售利润总和y与x的函数关系式;该专卖店经理应如何定价,才能使每月获得的月收益y最大?说明理由.
(1)当x=90时,女款T恤的月销量为
当50≤x≤90时?女款T恤的月销量为
当90≤x≤120时?女款T恤的月销量为
(2)若女款T恤的月销售量为100件,售价为多少元?
(3)求y1与x的函数关系式;
(4)若男款T恤月利润y2与x的函数关系式为:y2=20x+3000,求销售这款T恤的月销售利润总和y与x的函数关系式;该专卖店经理应如何定价,才能使每月获得的月收益y最大?说明理由.
考点:二次函数的应用
专题:
分析:(1)根据售价不超过90元时,价格每上涨1元,销售量减少1件,即可求得①当50≤x≤90时②当90≤x≤120时的函数式,即可解题;
(2)根据(1)中解析式将y=100代入,求得x的值即可解题;
(3)根据利润=销量×每件盈利,可得①当50≤x≤90时 ②当90≤x≤120时,利润的二次函数式,即可解题;
(4)分别对①当50≤x≤90时,②当90≤x≤120时,求得的二次函数值求最大值即可解题.
(2)根据(1)中解析式将y=100代入,求得x的值即可解题;
(3)根据利润=销量×每件盈利,可得①当50≤x≤90时 ②当90≤x≤120时,利润的二次函数式,即可解题;
(4)分别对①当50≤x≤90时,②当90≤x≤120时,求得的二次函数值求最大值即可解题.
解答:解:(1)∵售价不超过90元时,价格每上涨1元,销售量减少1件,
∴x=90时,月销量为80件,
故函数式为:当50≤x≤90时,女款T恤的月销量为y=-x+170;?
当90≤x≤120时,女款T恤的月销量为y=-2x+260;
故答案为 80,y=-x+170,y=-2x+260;
(2)当100=-x+170时,
解得:x=70,符合题意;
当100=-2x+260时,
解得:x=65,不符合题意;
故售价为70元;
(3)∵利润=销量×每件盈利,
∴①当50≤x≤90时,y1=(x-30)(-x+170)=-x2+200x-5100;
②当90≤x≤120时,y1=(x-30)(-2x+260)=-2x2+320x-7800;
(4)∵y=y1+y2,
∴①当50≤x≤90时,y=-x2+200x-5100+20x+3000=-x2+220x-2100,?
当x=110时,y有最大值,
∵50≤x≤90,
∴x=90时有最大值为:9600元,
②当90≤x≤120时,y=-2x2+320x-7800+20x+3000=-2x2+340x-4800,
当x=85时,y有最大值,
∵90≤x≤120,
∴x=90时有最大值为:9600元.
故专卖店经理应定价90元,能使每月获得的月收益y最大.
∴x=90时,月销量为80件,
故函数式为:当50≤x≤90时,女款T恤的月销量为y=-x+170;?
当90≤x≤120时,女款T恤的月销量为y=-2x+260;
故答案为 80,y=-x+170,y=-2x+260;
(2)当100=-x+170时,
解得:x=70,符合题意;
当100=-2x+260时,
解得:x=65,不符合题意;
故售价为70元;
(3)∵利润=销量×每件盈利,
∴①当50≤x≤90时,y1=(x-30)(-x+170)=-x2+200x-5100;
②当90≤x≤120时,y1=(x-30)(-2x+260)=-2x2+320x-7800;
(4)∵y=y1+y2,
∴①当50≤x≤90时,y=-x2+200x-5100+20x+3000=-x2+220x-2100,?
当x=110时,y有最大值,
∵50≤x≤90,
∴x=90时有最大值为:9600元,
②当90≤x≤120时,y=-2x2+320x-7800+20x+3000=-2x2+340x-4800,
当x=85时,y有最大值,
∵90≤x≤120,
∴x=90时有最大值为:9600元.
故专卖店经理应定价90元,能使每月获得的月收益y最大.
点评:本题考查了二次函数解析式的求解,考查了二次函数最大值的求解,本题中正确求得二次函数解析式是解题的关键.

练习册系列答案
相关题目
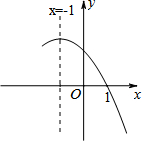 如图,下面是二次函数y=ax2+bx+c图象的一部分,则下列结论中,正确的个数是( )
如图,下面是二次函数y=ax2+bx+c图象的一部分,则下列结论中,正确的个数是( )①2(a+1)>2
②4a-2b+c>0
③方程ax2+bx+c=0有两个不等的实数根
④9a-3b+c=0.
| A、1 | B、2 | C、3 | D、4 |
等边三角形可以看作是自身的一个旋转图形,如果用它的两条角平分线的交点作为旋转中心,那么旋转角的度数是( )
| A、60° | B、120° |
| C、150° | D、180° |
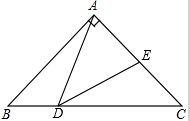 已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为
已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为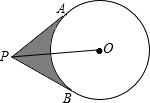 如图,已知P为⊙O外一点,PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长与面积.
如图,已知P为⊙O外一点,PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长与面积. 甲,乙两人在直线跑道上同起点,同终点,同方向匀速跑步500m,先到终点的人原地休息,已知甲先出发2秒,在在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,
甲,乙两人在直线跑道上同起点,同终点,同方向匀速跑步500m,先到终点的人原地休息,已知甲先出发2秒,在在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,