题目内容
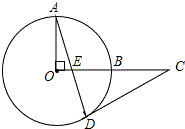 如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连接AD交OB于点E.求证:CD=CE.
如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连接AD交OB于点E.求证:CD=CE.考点:切线的性质
专题:证明题
分析:连接OD,根据切线性质求出∠ODC=90°,求出∠A+∠AEO=∠ODA+∠EDC=90°,求出∠CED=∠EDC,根据等腰三角形的判定推出即可.
解答: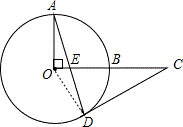 证明:连接OD,
证明:连接OD,
∵OA⊥OB,CD切⊙O于D,
∴∠AOE=∠ODC=90°,
∴∠A+∠AEO=90°,∠ODA+∠CDE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠AEO=∠EDC,
∵∠AEO=∠CED,
∴∠CED=∠EDC,
∴CD=CE.
 证明:连接OD,
证明:连接OD,∵OA⊥OB,CD切⊙O于D,
∴∠AOE=∠ODC=90°,
∴∠A+∠AEO=90°,∠ODA+∠CDE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠AEO=∠EDC,
∵∠AEO=∠CED,
∴∠CED=∠EDC,
∴CD=CE.
点评:本题考查了切线的性质,等腰三角形的判定和性质,三角形内角和定理的应用,解此题的关键是能正确作出辅助线,并推出∠EDC=∠CED,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为
已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为 一个物体的三视图如图所示,请画出该物体的形状.
一个物体的三视图如图所示,请画出该物体的形状. 如图,在梯形ABCD中,AD∥BC,△AOD的面积与△BOC的面积之比为1:9,△AOB的面积为6
如图,在梯形ABCD中,AD∥BC,△AOD的面积与△BOC的面积之比为1:9,△AOB的面积为6 如图,△ABC中,A,B,C三点的坐标分别是A(0,
如图,△ABC中,A,B,C三点的坐标分别是A(0,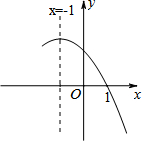 如图,下面是二次函数y=ax2+bx+c图象的一部分,则下列结论中,正确的个数是( )
如图,下面是二次函数y=ax2+bx+c图象的一部分,则下列结论中,正确的个数是( )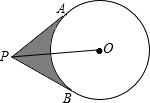 如图,已知P为⊙O外一点,PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长与面积.
如图,已知P为⊙O外一点,PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长与面积.