题目内容
6.如果关于x的一元二次方程x2-6x+2k=0有两个实数根,那么实数k的取值范围是( )| A. | $k≤\frac{9}{2}$ | B. | $k<\frac{9}{2}$ | C. | $k≥\frac{9}{2}$ | D. | $k>\frac{9}{2}$ |
分析 由方程有两个实数根结合根的判别式,得出关于k的一元一次不等式,解不等式即可得出结论.
解答 解:∵关于x的一元二次方程x2-6x+2k=0有两个实数根,
∴△=(-6)2-4×1×2k=36-8k≥0,
解得:k≤$\frac{9}{2}$.
故选A.
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是找出36-8k≥0.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出不等式(不等式组或方程)是关键.

练习册系列答案
相关题目
16.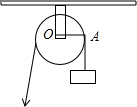 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点A旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )| A. | πcm | B. | 2πcm | C. | 3πcm | D. | 5πcm |
17.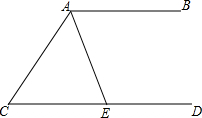 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
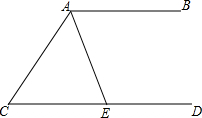 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )| A. | 65° | B. | 115° | C. | 125° | D. | 130° |
11.已知关于x,y的方程x2m-n-2+4ym+n+1=6是二元一次方程,则m,n的值为( )
| A. | m=1,n=-1 | B. | m=-1,n=1 | C. | $m=\frac{1}{3},n=-\frac{4}{3}$ | D. | $m=-\frac{1}{3},n=\frac{4}{3}$ |
15.-1是1的( )
| A. | 倒数 | B. | 相反数 | C. | 绝对值 | D. | 立方根 |
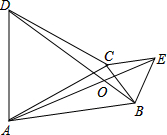 如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为120°.
如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为120°.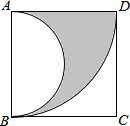 如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则阴影部分面积是2π(结果保留π).
如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则阴影部分面积是2π(结果保留π).