题目内容
12. 如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将$\widehat{CD}$沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将$\widehat{CD}$沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为$\widehat{ADB}$的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交$\widehat{BC}$于点F(F与B、C不重合).问GE•GF是否为定值?如果是,求出该定值;如果不是,请说明理由.
分析 (1)连接OC,根据翻折的性质求出OM,CD⊥OA,再利用勾股定理列式求解即可;
(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根据圆的切线的定义证明即可;
(3)连接GA、AF、GB,根据等弧所对的圆周角相等可得∠BAG=∠AFG,然后根据两组角对应相等两三角相似求出△AGE和△FGA相似,根据相似三角形对应边成比例可得$\frac{AG}{GE}$=$\frac{FG}{AG}$,从而得到GE•GF=AG2,再根据等腰直角三角形的性质求解即可.
解答  (1)解:如图,连接OC,
(1)解:如图,连接OC,
∵$\widehat{CD}$沿CD翻折后,点A与圆心O重合,
∴OM=$\frac{1}{2}$OA=$\frac{1}{2}$×2=1,CD⊥OA,
∵OC=2,
∴CD=2CM=2$\sqrt{O{C}^{2}-O{M}^{2}}$=2$\sqrt{{2}^{2}-{1}^{2}}$=2$\sqrt{3}$;
(2)证明:∵PA=OA=2,AM=OM=1,CM=$\frac{1}{2}$CD=$\sqrt{3}$,∠CMP=∠OMC=90°,
∴PC=$\sqrt{M{C}^{2}+P{M}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{3}^{2}}$=2$\sqrt{3}$,
∵OC=2,PO=2+2=4,
∴PC2+OC2=(2$\sqrt{3}$)2+22=16=PO2,
∴∠PCO=90°,
∴PC是⊙O的切线;
(3)解:GE•GF是定值,证明如下,
连接GO并延长,交⊙O于点H,连接HF
∵点G为$\widehat{ADB}$的中点
∴∠GOE=90°,
∵∠HFG=90°,且∠OGE=∠FGH
∴△OGE∽△FGH
∴$\frac{OG}{GF}$=$\frac{GE}{GH}$
∴GE•GF=OG•GH=2×4=8.
点评 本题是圆的综合题型,主要利用了翻折变换的性质,垂径定理,勾股定理,勾股定理逆定理,圆的切线的定义,相似三角形的判定与性质,难点在于(3)作辅助线构造出相似三角形.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | $\frac{1}{7}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{21}$ | D. | $\frac{1}{10}$ |
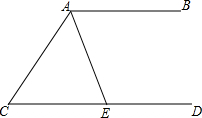 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )| A. | 65° | B. | 115° | C. | 125° | D. | 130° |


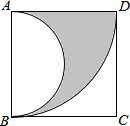 如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则阴影部分面积是2π(结果保留π).
如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则阴影部分面积是2π(结果保留π). 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: