题目内容
2.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如表:| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 70 |
| 每天销量(件) | 200-2x | |
(1)当1≤x<50时,求出y与x的函数关系式;
(2)问销售该商品第几天时,销售利润最大,最大利润是多少?
分析 (1)根据单价乘以数量,可得利润,可得答案;
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案.
解答 解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;
(2)当1≤x<50时,
y=-2x2+180x+2000,
y=-2(x-45)2+6050.
∴a=-2<0,
∴二次函数开口下,二次函数对称轴为x=45,
当x=45时,y最大=6050,
当50≤x≤90时,
y=(200-2x)(70-30)=-80x+8000,
∵y随x的增大而减小,
∴当x=50时,y最大=4000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
点评 本题考查了二次函数的应用,利用单价乘以数量求函数解析式,利用了函数的性质求最值.解答时求出函数的解析式是关键.

练习册系列答案
相关题目
10. 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
7.已知m为实数,且sinα、cosα是关于x的方程3x2-mx+1=0的两根,则sin4α+cos4α的值为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
11.某中学为了解九年级学生的身体素质情况,随机抽查了九年级部分学生一分钟跳绳次数,绘制成如下统计图表(图1,图2,表).
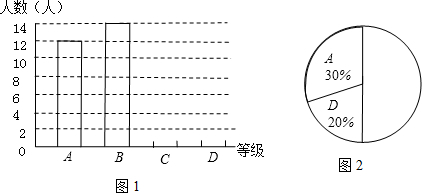
请结合图表完成下列问题:
(1)表1中a=6,b=8;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为200人.
| 等级 | 一分钟跳 绳次数x | 人数 |
| A | x>180 | 12 |
| B | 150<x≤180 | 14 |
| C | 120<x≤150 | a |
| D | x≤120 | b |

请结合图表完成下列问题:
(1)表1中a=6,b=8;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为200人.
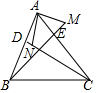 如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.
如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.