题目内容
1.(1)解方程:①x2+4x-12=0;②3x2+5(2x+1)=0(2)已知|a-2|+$\sqrt{b-3}$=0,计算$\frac{{a}^{2}+ab}{{b}^{2}}•\frac{{a}^{2}-ab}{{a}^{2}-{b}^{2}}$的值.
分析 (1)①把方程左边化为两个因式积的形式,求出x的值即可;
②先把方程化为一元二次方程的一般形式,利用公式法求出x的值即可;
(2)先根据非负数的性质求出a、b的值,再根据分式混合运算的法则把原式进行化简,把a、b的值代入进行计算即可.
解答 解:(1)①∵原方程可化为(x-2)(x+6)=0,
∴x-2=0或x+6=0,
∴x1=2,x2=-6;
②原方程可化为3x2+10x+5=0,
∵△=100-4×3×5=40,
∴x=$\frac{-10±\sqrt{40}}{2×3}$=$\frac{-5±\sqrt{10}}{3}$,
∴x1=$\frac{-5+\sqrt{10}}{3}$,x2=$\frac{-5-\sqrt{10}}{3}$;
(2)∵|a-2|+$\sqrt{b-3}$=0,
∴a-2=0,b-3=0,
∴a=2,b=3.
原式=$\frac{a(a+b)}{{b}^{2}}$•$\frac{a(a-b)}{(a+b)(a-b)}$
=$\frac{a(a+b)}{{b}^{2}}$•$\frac{a}{a+b}$
=$\frac{{a}^{2}}{{b}^{2}}$,
当a=2,b=3是,原式=$\frac{4}{9}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
9.在今年的“希望工程”捐款活动中,某班级一小组7名同学积极捐出自己的零花锇,奉献自己的爱心,他们捐款的数额分别是(单位:元)5O、20、5O、30、25、50、55,这组数据的众数和中位数分别是( )
| A. | 50元,30元 | B. | 50元,40元 | C. | 50元,50元 | D. | 55元,50元 |
16.下列各图中,∠1与∠2是对顶角的是( )
| A. | 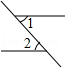 | B. |  | C. | 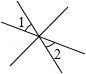 | D. | 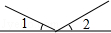 |
10.观察下列一组图形中黑点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第16个图中共有点的个数是( )
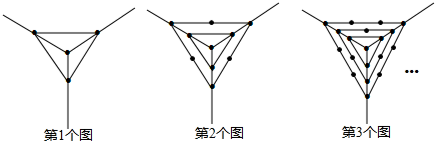

| A. | 408 | B. | 409 | C. | 361 | D. | 360 |
 如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠1和∠4,∠2的对顶角是∠3.
如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠1和∠4,∠2的对顶角是∠3.