题目内容
11.阅读下列材料,并按要求完成相应的任务.
任务:
(1)如图2,是5×5的正方形网格,且小正方形的边长为1,利用“皮克定理”可以求出图中格点多边形的面积是7.5;
(2)已知:一个格点多边形的面积S为15,且边界上的点数b是内部点数a的2倍,则a+b=24;
(3)请你在图3中设计一个格点多边形(要求:①格点多边形的面积为8;②格点多边形是一个轴对称图形但不是中心对称图形)
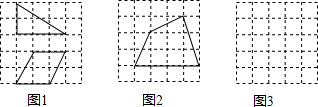
分析 (1)直接利用“皮克定理”得出多边形的面积;
(2)利用“皮克定理”结合S的值以及a,b的关系得出答案;
(3)利用轴对称图形的定义结合各点多边形的定义得出答案.
解答 解:(1)由“皮克定理”可得:S=5+$\frac{7}{2}$-1=7.5;
故答案为:7.5;
(2)∵S为15,且边界上的点数b是内部点数a的2倍,
∴a+$\frac{2a}{2}$-1=15,
解得:a=8,则b=16,
故a+b=24,
故答案为:24;
(3)如图所示: .
.
点评 此题主要考查了轴对称变换和新定义,正确理解“皮克定理”是解题关键.

练习册系列答案
相关题目
3.某超市计划购进甲、乙两种品牌的新型节能台灯20盏,这两种台灯的进价和售价如下表所示:
设购进甲种台灯x盏,且所购进的两种台灯都能全部卖出.
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
| 甲 | 乙 | |
| 进价(元/件) | 40 | 60 |
| 售价(元/件) | 60 | 100 |
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
 有一道作业题:解方程$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$.下面的纸片上是小明的解答过程:
有一道作业题:解方程$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$.下面的纸片上是小明的解答过程: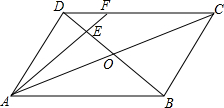 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.